Someone (I’m not sure if they want to be named, so I won’t, but they’re welcome to comment if they wish) sent me a copy of a document by David Wasdell. It’s called Sensitivity and the Carbon Budget, and is an attempt to determine the Equilibrium System Sensitivity (ESS). Both the person who sent it to me, and myself, think they should try and get it published, but they seem to want some kind of feedback. So, this post is an attempt to get my highly-educated and well-informed commenters to provide some kind of pre-submission review.
I’ll provide some comments to get it started. The basic premise is that doubling CO2 produces a change in forcing of 3.7 Wm-2 and, by itself, would increase surface temperatures by 1oC. The temperature change between the last ice age and the pre-industrial Holocene is about 5oC. This would then (given 3.7 Wm-2 ~ 1oC) be associated with a change in radiative forcing of 19 Wm-2.
Over the same time period atmospheric CO2 concentrations increased from 180ppm to 280ppm which would produce a change in radiative forcing of
This is 8 times smaller than the net change in radiative forcing, therefore (according to David Wasdell) feedbacks must amplify this by a factor of 8. If we now consider a doubling of CO2, which produces a change in radiative forcing of 3.7Wm-2, feedbacks would increase this to 30Wm-2 and – hence – the ESS would be about 8oC.
So, that’s roughly what’s presented in the paper. I have two basic comments. One is that the driver for the change from the last ice age to the Holocene was not simply increased atmospheric CO2. It was probably variations in our orbit and variations in the inclination of our axis. It’s thought that this produced an enhanced forcing in the northern hemisphere (above 65N) which melted ice and reduced the albedo. This then warmed the planet and released CO2. The CO2 then produced further warming, increasing the melting which then reduced the albedo further and further increased CO2 concentrations. So, it was a combination of changes in our albedo and increases in atmospheric CO2 – and other greenhouse gas (GHG) – concentrations.
If you look at Figures 5 and 6 in this paper (Hansen & Sato) the external forcings are taken to be both GHGs and albedo changes. My understanding is that it is hard to separate these two effects and, since they’re both slow, by combining them (to get a total change of around 5-6 Wm-2) you get an estimate of the Equilibrium Climate Sensitivity (ECS) which is essentially a response to fast feedbacks only. Given a change in temperature of 4-5oC and a change in forcing of 5-6 Wm-2, you get a climate sensitivity of 0.75oC per Wm-2; or around 3oC per doubling.
Since it’s hard to separate the GHGs and the albedo changes, it’s quite hard to actually determine – robustly – an ESS. The one extreme would be what’s been done in David Wasdell’s work. Assume that one of them is the main external forcing and the other is a feedback, which gives an ESS of 8oC. Alternatively, assume that they combine to give a net change in external forcing, which then gives an ESS of 3oC. As I understand it, the best that we can say is that it is probably somewhere inbetween (although, I’m happy to be corrected here as this is somewhat outside my comfort zone).
The other comment I was going to make is that if you assume that the feedback response is some fraction 
If the feedbacks amplify the external forcing by a factor of 8 (as suggested by David Wasdell), then 
Anyway, those are my thoughts based on a fairly quick reading of the document. My gut feeling is that it is too simplistic and doesn’t appreciate that CO2 was not the only external forcing that warmed us from the past ice age into the Holocene. I’m also sure there’s much more that could be said, including the difference between the ECS and ESS timescales and whether that is relevant or not. So, maybe some others who know more about this than I do, could have a look and provide some feedback through the comments.
...and Then There's Physics 
I didn’t read too carefully (hey, this is the wub) but “the ESS would be about 8oC” sounds awfully close to Hansens “the ESS is 6 oC”. You’d want to make sure that you’ve carefully looked at those arguments and that you’re not just repeating them.
William,
I presume you mean the author, not me (and it really isn’t me 🙂 ). Yes, that is a good point. I haven’t actually looked at Hansen’s argument for the ESS being 6oC, but had rather assumed that it had to be bigger than the ECS (3oC) but couldn’t really be as high as the 8oC suggested in this document. Of course, I should probably have an actually look at what Hansen is suggesting, rather than just guessing 🙂 .
Here’s a link to Hansen et al. (2008) that produces an estimate for the ESS. My quick reading suggests that William may have a point. It seems to already have broadly done what David Wasdell is trying to do and, probably, has done it a bit more accurately.
Anders, the links to the author and to the paper give his name as “David Wasdell” not David Harris.
Ian,
Thanks. No idea where the Harris came from. One of my many moments of confusion 🙂
Re Hansen, don’t miss http://scienceblogs.com/stoat/2007/11/23/hansen-again/ or at least the comment someone made that the paper was “like being inside Hansens head”.
Or that f is not fixed; that it varies with regard to the starting point.
For instance, you only get the big feedback from melting ice and its associated albedo once. Once all the ice is melted, further increases in temperature don’t get to use that feedback any more. (And the paper does address this).
This is relevant: Previdi et al. (2013) as it is I think the most recent paper investigating ESS which has Hansen as a co-author.
Windchaser,
Indeed, that would be possible. In fact, I think that one of the arguments in Hansen et al. is that it will depend on the ice coverage. So, we might expect it to be smaller today than in the last ice age as we have less ice coverage now than we had then. All I was really suggesting was that maybe we wouldn’t expect it to be very close to 1. A simplistic argument, I accept.
BBD,
Thanks. It seems to me that this has all already been done.
BBD,
Figure 2 in the paper you link to is quite informative as it gives both the sensitivities and the timescales.
William,
Thanks, I’ll have to try and read that paper and the blog comments. Barbecue time first though!
I think you actually ought to reverse the argument “we’ve had major changes to our climate in the past without a runaway occurring, […] suggest that f cannot be this close to 1.” As Windchaser says, f is not a fixed number. And the fact is, we’ve had major changes to our climate in the past with VERY LITTLE change in input forcing (the change in CO2 associated with glaciations and interglacials is a feedback itself, not a forcing). The relatively rapid transitions between glacial and interglacial state are almost indicative of a long-run instability (f > 1). Note that feedback is a time-dependent thing in the first place, which is why ESS is different from ECS etc.
Arthur,
isn’t constant. However, surely averaged over a reasonable timescale 
can’t exceed 1, or am I missing something here?
Sure, I agree that
Excellent lead-in to the topic, perhaps the most readable and succinct explanation of climate sensitivity I have seen. What comes to my mind is a logistic curve for the feedbacks rather than linear, and also some hysteresis. My thinking is that the phase transitions of water create natural boundaries for the limits of feedbacks, and since the earth is approximately spherical, these phase transitions are already engaged at some point on Earth, producing an “s” shaped feedback curve (logistic curve) rather than linear. As the Earth cools, more and more of it will simply stop participating in feedback changing the slope of the sensitivity.
Going the other way one might suppose a logarithmic curve leading to thermal runaway but upper bounds would seem to exist, several actually. I suspect the main upper bound is water condensation cycle into clouds.
In the steepest part of the logistic curve the feedback amplification is probably pretty steep.
I suspect the abrupt transitions to and from interglacial periods relates not only to the steepness of this feedback curve between its boundaries but also to hysteresis. Just as a cup of water can be slowly cooled below 0 C and still be liquid, or raised above 100 C and still be liquid, until a physical event happens to suddenly trigger a phase transition, so too might the Earth go beyond a gradual cooling into a glacial period becoming increasingly sensitive to a trigger that brings on a glacial period.
As to the paper itself — a bit too religious, I mean really, Apollo and Gaia as proxies for Sun and Earth? As I look into it I realize it is all “agenda” and almost no science. I’ve only gotten to page 4 — no citations or footnotes but plenty of reference to Club of Rome. The provenance is the Meridian project, an extremely left wing social change thing. Policy and conclusion precedes science (Well, that is likely often the case but normally you don’t brag about it).
“your core temperature is itself more or less sensitive to the effects of certain pathogens or infections. As with your body, so with the planet.”
I see. Earth raises its temperature to get rid of pathogens (that would be you and me).
“While the global average has increased by 0.85° C, the Arctic temperature has risen by about
3° C. Area and volume of end-of-summer floating sea-ice are collapsing. ”
Citations, footnotes, anything? Any mention of Antarctic ice growing?
“The object of the “Unit for Research into Changing Institutions” … Unit resources were focussed almost exclusively on the Climate Change agenda.”
http://www.apollo-gaia.org/A-GProjectDevelopment.pdf (top of page 4, read the paragraph to see whether … eliminates anything substantially changing the meaning)
The purpose of this person and group is to change society. That is why they fail. Many people think they can change society and tend thereby to cancel each other out.
While this paper doesn’t seem useful, studying the history of the writer is fascinating. I sense genuine fear and panic in these few persons that seem to believe they alone can Save The Earth. This is one of a few Big Questions that has been on my mind for many years — WHY are some people willing to impose a totalitarian, one-world government? FEAR.
“Must now consider ourselves on a War Footing, with implications for industry and the civil society. There will inevitably be winners and losers.”
http://www.apollo-gaia.org/A-GProjectDevelopment.pdf (page 23).
M2 – as has been pointed out in many places at many times, losing arctic sea ice changes albedo in the months of largest insolation. Gaining antarctic sea ice is nearly the exact opposite – increasing albedo in the months of least insolation. Therefor, one has a significant impact on the earth’s energy budget the other has very little effect.
M2,
I haven’t looked into the author’s background. Maybe you can illustrate how you’ve concluded this is one of his goals. I must admit that there are some who seem to conclude that a suggestion that “Climate Sensitivity might be high” immediately implies that the person making the suggestion is a socialist who wants to impose some kind of totalitarian, one-world government. Maybe you can help me to understand why some people seem to jump to this conclusion. I have yet to see a good explanation for this (well, not one that doesn’t make the person jumping to the conclusion seem like a bit of a twit).
No, that’s right. If f > 1 over a given timescale, then any forcing will result in an infinite increase in temperature.
However, the change in temperature for a change in forcing could be rather large, so long as it only held over a relatively small range of temperatures.
Windchaser,
You may have to explain that as I’m not quite sure I’m getting what you mean here.
Hmm…
Sounds like Monkton gone over to the other side…
Seriously, though, the paper makes a couple of good points
– AR5 is focussed on relatively short term impacts (to 2100) which implies policy based on it will lock in longer term impacts
– ECS is actually a very conservative measure of impact
– and in the round it generally makes the point that AR5 is in fact, far from alarmist, actually a very conservative document
However,
– I think it cherrypicks numbers to make ESS look large
– it mentions but fails to build into the quantification that the absence of large continental icesheets must reduce ESS in the future from the number from LGM to now
And I meant to add that the generally florid language instantly removes technical credibility (see quote above)
Here is my comment based on a quick read. I think it would be very hard to get this published in its present form. It definitely does not conform to the way most experts think about this problem — it seems to combine forcing feedbacks in an odd (and I think, but am not sure, wrong) way. I suspect that most reviewers would barf all over it. And I think that, as pointed out above, Hansen basically already did this calculation.
Much of this is already covered but:
1) Hansen has already done this calculation, and done it better (although I am not certain he did in a paper published other than in arxiv;
2) Hansen did it better because he included not only CO2 but forcing from CH4 as well, lifting the “initial” forcing to 3 W/m^2 (which drops the ESS to 6.2 C per doubling of CO2).
3) I consider even that dubious in that the initial forcing was actually a change in albedo, so that the change in albedo is a more appropriate measure for calculating ESS from the LGM. The change in albedo is 3.5 W/m^2, yielding an ESS of 5.3 C per doubling of CO2.
4) Better yet would be to acknowledge the fact that changes in forcing have different effects on mean global temperatures depending on geographical location and season, and determining a weighted forcing based in the initial milankovitch forcing, from which to determine the ESS. I am not sure, however, that this approach is either tractable, nor non-circular for determining sensitivities.
5) Regarding the high f for a ESS of 8, Park and Royer (2011) determine an ESS of 3-4 C across the phanerozoic, but 6-8 C when there is widespread glaciation. That would indicate a significant risk of runaway cooling, consistent with at least to snowball Earth episodes in Earth’s history, but no significant risk of runaway warming. Similar figures to those by Park and Royer are found by a number of researchers, as listed by Royer et al (2012), Table 1.
Anders,
However, the change in temperature for a change in forcing could be rather large, so long as it only held over a relatively small range of temperatures.
“Change in equilibrium temperature for a change in forcing” is just the derivative of equil. temps with respect to forcing.
I’m saying this derivative can be high, that the temperature of the system might be quite sensitive with respect to an infinitesimally small change of forcing, but if this high sensitivity holds over a very large range of temperatures, we’d see very large swings in temperature for any perturbation.
As it is, we generally don’t see that. IIUC, climate is more indicative of either a monostable system (depending only on forcings) or bistable system (depending both on forcings and initial conditions, giving us glacial and interglacial periods). When we’re at a given climate state, as over the last 10,000 years, we don’t tend to see large swings in temperature for small changes in forcings.
OT: Anyone who thinks the failure in the U.S. to advance quickly enough on climate policy is in any way the fault of scientists should read this, although I suppose it’s hard to deny that it would help if scientists were to become less naive about the nature of the policy process.
M2: Your obsession about the mythical ‘world government’ boogeyman continues to cloud your ability to accept the reality of man made climate change.
And Then There’s Physics says: “I haven’t looked into the author’s background. Maybe you can illustrate how you’ve concluded this is one of his goals”
Off and on throughout the day I have responded to your question, erased it, started over, erased it again. It’s a big topic and just doesn’t fit on this page. His CV is easy to find and rather interesting (far removed from science), his association with Joachim Schellnhuber and PIK is easy to find and relevant to your question.
More relevant to me was feeling that he is the genuine article, he’s afraid for the future and thus perfectly willing to consider depriving me of liberty as an ethical choice. Persons that are in it for the money tend to avoid publishing theories of depriving liberty, rather, they pursue financial goals (Schellnhuber is a banker and a physicist, a strange combination but there you go, why not a really smart banker?) sometimes using government mandates to ensure profitability, or so it seems to me.
Re: And Then There’s Physics, global government.
One more try at it. I keep losing context during my reply.
The problem is conflation — the goals of stop-the-warming advocates and the goals of global government advocates overlap, so much so that some long-time advocates of global government have embraced global warming as a way to achieve this outcome.
So my reference isn’t to David Wasdell per se or specifically, but rather an opportunity to try to understand (1) the fear mechanism of global warming advocacy and (2) how this translates or is used by global governance advocates.
Persons with known qualifications in psychology include this author and also Lewandowsky; used for their skill in shaping a message of fear. It is better, in fact, for these authors to NOT have a solid science background the better for them to *believe* what they write, and that conviction then comes through as passion. I believe many people are persuaded almost entirely by the passion of the believer (hence young church missionaries) particularly where the truth of a claim is difficult to impossible to verify.
In the case of David, he alludes to this global governing in his paper since he recognizes that conflict is inevitable. There will either be conflict forming a global government, or if successful with that, more conflict as it tries to do the impossible — regulate 7 billion people.
But some people feed on conflict (arbitrage comes to mind). But that’s a topic for a different day.
Lubos Motl had what seemed to me to be a reasonable argument for why f cannot be too high.
ATTP: Page 3 of http://www.apollo-gaia.org/A-GProjectDevelopment.pdf provides the most direct information to your question for me.
“Drawing on three decades of consultancy-research focussed on the psychodynamics of social systems facing rapid change in conditions of low resource and high stress, I began to explore how best to consult to the process. A three-part paper entitled ‘Global Warning’, was prepared in order to begin to raise awareness of this agenda of social psychology.”
That’s what it is — social psychology. Scary words, charts and graphs with no distracting footnotes and citations. It doubtless includes some science but is carefully chosen and worded not as a scientific report of new discoveries but for public consumption and to stimulate “change”.
“Initial literature search, correspondence and conversations led to an early approach to John Schellnhüber, the Director of PIK Potsdam.”
I wonder why he wrote John rather than Joaquim Schellenberger?
He was also highly inspired by Jim Lovelock (of Gaea fame) but the latter has since distanced himself from the “living organism” view of Earth.
“Today we recognise that those in possession of the most accurate information share the
greatest responsibility for ensuring its most effective application.”
Or, since I am so much smarter than you, I will tell you what to do and when to do it.
“The Club of Rome, on the other hand, with its unique constitution, its history, its global connectivity and its reputation for the highest quality of scientific investigation and disinterested application, may well be best placed to take up the critical agenda now facing the global community. ”
Well, there you have it. Aligned with the Club of Rome, “disinterested application” if you can believe it (I don’t). David provides the scary words and pictures, the Club of Rome is who David means by what is to be done and who best to do it. So mosey on over to Club of Rome and check out the agenda.
Whups – Schellnhuber.
For what it’s worth, to M2’s point, pretty sure Wasdell is part of AMEG, the “Arctic Methane Emergency Group”, which promotes some pretty extreme climate stuff – and emergency, immediate deployment of geoengineering in the Arctic. Fellow AMEG member Peter Wadhams contributed to the article in Nature last year which was – by all accounts by leading carbon cycle experts like David Archer – rubbish. The scenarios modelled (economically, but based on Wadhams’ physical scenario speculations) were all but ruled out this century by IPCC AR5 WG1.
Just saying. Not that the paper at hand is flawed.
With respect to Hansen’s ESS work, Myles Allen raises some valid criticisms/caveats, iirc – but that was some years ago. Maybe never published/came-to-anything. I will check.
Motl’s argument (and I think ATTP’s confusion here) depends on two things that are not correct.
First, for any definition of feedback, a timescale most be involved. Motl assumes the timescale is decades – that is appropriate for feedbacks involved in short-term (transient) response. But the processes associated with ECS are century-scale at least, and for ESS (primarily the ice-sheet albedo changes) millennium-scale. So there’s one or two orders of magnitude separation in the timescale for exponential growth, if we were in an “f > 1” scenario.
But second – “f > 1”, if it depends on things like ice sheet albedo feedbacks, is self-limiting. On the cooling side, there is only so much Earth surface area for ice sheets to grow; on the warming side similarly once the ice sheets are gone, that feedback term is gone. So the “f > 1” scenario, if it happens, only applies for (effectively) a limited range of global average temperatures. If global average temperature is too high, most of the ice sheets have melted and the marginal rate of change in response to a further increment in temperature gets smaller. Similarly if global average temperature is too low, there are presumably also self-limiting effects from too much surface area covered already so there’s not much more effect that can be obtained (the snowball case is clearly a limit, but presumably the feedback level is reduced before you reach the full snowball Earth).
Now there is a runaway scenario for “f > 1” that has very different limits – that’s when temperatures get so high that we’re starting to boil the oceans; the Venus situation. Hansen has expressed worries about this for Earth and I don’t think he’s the only one. Clearly that has never happened previously in Earth’s history, but since our Sun has been gradually warming it’s something that will over time become more and more likely, as water vapor feedbacks naturally increase with average temperature.
RB, actually it is a very poor argument. He arbitrarily assumes that f > 1 will result in a runaway of Global Mean Surface Temperature (GMST) to levels that would result in a snowball Earth or a runaway greenhouse effect within 47 years, a figure that completely ignores both the heat capacity of the oceans and the rate of feedbacks (some of which a very slow in human terms). He further arbitrarily assumes that any runaway event will result in total extinction of life on Earth,which may be a fair assumption for runaway greenhouse, but is not for snowball Earth conditions, under which there will be refugia for simple life near volcanic vents and other geothermal hot spots. Finally, he declares that no runaway events have occurred in Earths 4.7 billion year history despite the clear evidence of at least two snowball Earth events, the most recent of which ended about 0.53 billion years ago. Further, even the 4.7 billion years is an exaggeration in that we only have clear evidence of life existing on Earth for the last 3.8 billion years, and are fairly certain it did not exist more than 4 billion years ago.
In essence, Motl has assumed a spherical cow, and use that assumption to prove cows don’t have legs.
The PALAEOSENS project (Rohling et al. 2012) concluded that over the last 65 million years, ECS has been 2.2–4.8C per CO2 doubling. As noted, “f” is larger at lower temperatures with more ice albedo feedback. That’s why a study over the last 65 million years is informative, because for most of that time Earth was even warmer than now. Estimates of “f” during glacial times aren’t relevant to the next millenium. Rohling et al. 2012 seem to have computed Charney (ECS) climate sensitivity by subtracting slow feedbacks like ice albedo.
Arthur,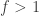
for some period, but it will not runaway because that feedback will eventually halt.
Thanks, yes, I think I see what you mean. Certain feedbacks are self-limiting and therefore
Windchaser,
Thanks. Yes, that makes sense.
Science of Doom had recently a series of posts on glacial cycles, where he reviewed a large number of papers on the subject. Based on all that, my impression is that the concept of (linear) feedback is totally unsuited for understanding the history. My own interpretation of the history is that the persistent states of the Earth history are not the end points of the cycles (maximum and minimum glaciation or temperature) but the states of transition in either direction.
Most of the time the Earth has been in the state of increasing glaciation, decreasing temperature, and decreasing CO2 concentration. These long periods have been interrupted by warm phases of Milankovitch cycles, but persisted and continued until a relatively short-lived state of maximal ice-cover is reached. The following state of deglaciation is shorter as deglaciation proceeds faster and essentially without interruption reaching the other short-lived turning point of interglacial. The recent papers of Abe-Ouchi and others describe possible mechanisms for this kind of behavior.
If that overall picture is correct, we cannot expect to learn much on the strength of feedbacks from the glacial history. The history tells in this interpretation that in some sense f > 1 most of the time, but less during the interglacial as it would represent a natural extreme point of the cycle. Changing the amount of CO2 participating in the cycle would probably change the properties of this extreme state, but the argument cannot tell (from present knowledge), what the size of the change would be. The relevant ESS is essentially this change as we are near the interglacial turning point (probably past the turning point of the natural cycle, but still in the period that precedes the real onset of cooling).
> My own interpretation of the history is that the persistent states of the Earth history are not the end points of the cycles (maximum and minimum glaciation or temperature) but the states of transition in either direction.
That’s really cute, and I like it. A nicely different way of looking at things.
I’m still trying to understand the subtlety of it 🙂
The proposal has many implications. Rather than asking as primary question, what initiates glaciation, natural primary question are now:
– What’s the set of dynamic relationships that make the phases of glaciation and deglaciation persistent?
– What stops these phases? For the present interglacial that implies more detailed questions:
– – Why the interglacial has the particular temperature it has?
– – Why do we still have continental ice sheets and why their extent is the present one?
– In that picture the interglacial is fundamentally unstable or metastable. What limits the length of that metastable period?
Milankovitch cycles have less role in this picture. The shorter Milankovitch cycles up to 40 kyears do certainly affect the climate, but even they would not be the main driver of glacial cycles. They might contribute as the ultimate trigger, when the system is ready for getting triggered.
ATTP
Me too. It feels as though you have to set up something rather close to a strawman about Milankovitch in order not simply to see the things Pekka mentions above as aspects of the full complexity of the glacial/deglacial cycle.
Spatial/seasonal insolation change (orbital); ice sheet dynamics; ice albedo change; effects of same on coupled ocean/atmospheric circulation; effects of same on CO2 (ocean reservoirs) and CH4 (wetlands) etc. It’s all of a part.
BBD,
I may well be misunderstanding Pekka’s point, but I think it depends on how you regard the role of this complexity. We know that the climate isn’t extremely sensitive to small changes in global forcing. However, variations in our orbit that produce very small global changes in forcing, seem to trigger substantial changes in our climate. Is that because there’s a large local change which then acts as the driver, or is it because the system simply needs a small push in order to trigger a change that then proceeds because of ice sheet dynamics, etc.? Again, maybe I haven’t quite got the subtlety of what Pekka is suggesting.
BBD and ATTP,
If you haven’t read trough the posts of SoD and discussion there, I propose that you do.
The case for the dominance of Milankovitch cycles in controlling the glacial cycles does not seem to be strong. There’s no doubt that the precession and obliquity cycles with periods close to 20 kyear and 41 kyear affect climate, but explaining glacial cycles is much more controversial. The idea that internal properties of the Earth system may well be more important factors in the determination of the length and properties of the glacial cycle. That’s certainly what the data looks like, and Abe-Ouchi has proposed a more specific mechanism that might be the explanation.
Pekka,
Yes, I have read quite a few of those and am aware of the issues related to how Milankovitch cycles are triggered.
I think it’s well worth remembering that orbital dynamics seem to account for both deglaciation *and* the slide back into glacial conditions. Yes, the climate comes out of a glacial relatively fast compared to the slide back into glacial conditions, so yes, ice sheets would seem to be implicated in the speed of the deglacial response but perhaps not the overall sensitivity of the climate system to variations in insolation.
Pekka
I have. With particular note of what Steve Bloom posted.
Only if you all-but create a strawman.
You both have asked, what I’m proposing as the alternative. What I propose is significantly different from emphasizing strongly the Milankovitch cycles, it’s significantly different, whether it’s correct or not.
While neither SoD nor myself is a specialist on glacial cycles, I do believe that SoD has demonstrated well, that the issues is a controversial one also for the specialists (this has nothing to do with climate skepticism, but is purely an issue of science).
I don’t know, what you want to say by reference to what Steve Bloom posted. He has certainly also referred to Abe-Ouchi, and I haven’t thought that his understanding is very different from mine on that.
I presume the Abe-Ouchi work you mean is this one. I don’t know enough to judge it, but what the abstracts say doesn’t seem particularly controversial. It seems clear that the orbital variations are small, but they still seem to play a big role in determining the timing of the changes, even if they don’t determine the rate at which they’re changing.
ATTP,
As usual, the wording is careful, but the paper describes, how the hysteresis type phenomena could be the main controlling factor of the length of the cycle.
Basically the phase of glaciation ends when it has persisted for long enough, not when the Milankovitch eccentricity cycle forces it to end.
Pekka:
I disagree – it’s exactly what climate scepticism should be. What is has nothing to do with is climate ‘scepticism’.
I remember trying to compose a list of genuine climate sceptics a year or two back. I came up with two potential candidates, Science of Doom and yourself.
OPatrick,
I presume you have some kind of definition for the term “climate sceptic” 🙂
Hmm, probably something like ‘people who regularly ask genuinely challenging questions about areas of science that a non-expert such as myself might perceive as being broadly settled and can demonstrate in further discussion that this questioning is not obviously motivated by non-science based reasons’.
Or the other answer would be ‘no’.
Oh, by the way, in case there was confusion, the ‘yourself’ was referring to Pekka – I see that is ambiguous.
Not that you don’t display genuine scepticism. Just that the tenor of your writing suggests conviction, on balance.
It’s getting dark in here. I’ll put the spade down.
OPatrick,
I was just suggesting that most climate scientists probably ask genuinely challenging questions about areas of science that a non-expert might perceive as challenging 🙂 . Of course, if you restrict it to the blogosphere, then I think you’re probably right. There aren’t many who actually challenge our current understanding of climate science in a way that is scientifically credible. I would agree that two names that immediately spring to mind are indeed Pekka and SoD.
As I understand the theory: According to these “experts” there are one forcing agent, CO2, and several feedback mechanisms that caused the melting of ice age. CO2 is the real melting agent, and is nearly 100% responsible for what happened. It all can be traced back to some increase of CO2. A dry and cold planet Earth was changed into a wet and warm planet Earth by some mysterious mechanism started by some tiny changes of the CO2 consentration. There is no scientific consensus how this could happen, but we have to believe it. Let us also believe that there are no other mechanisms that can warm ocean, change the ocean currents increase water vapor. change ozone consentration etc.
Nobodyknows,
No, you don’t really. Try reading some of the other comments and maybe some of the papers.
nobodyknows
CO2 and CH4 are feedbacks to orbital forcing.
As ATTP said, perhaps read first and comment later. Try this; it’s very good.
Nobodyknows:
“As I understand the theory: According to these “experts” there are one forcing agent, CO2, and several feedback mechanisms that caused the melting of ice age.”
Would you do us a favor and change your handle to “Idontreadscience” because what you have posted is in no way even close to representing what science tells us. As BBD says, in this context CO2 is thought to be a feedback to orbital forcing, and further the fact that it is a feedback is what leads to the factoid so beloved by denialists – “CO2 increases are caused by warming, not vice-versa”.
You can’t intelligently criticize what you totally misunderstand, so until you display some basic understanding you’re not going to be taken seriously in knowledgeable circles. Though I’m sure folks at WUWT and the like applaud your misrepresentations …
I suppose viewing Earth’s history as a glacial-interglacial oscillation can be viewed under a linear feedback analysis as f>=1. It seems to me that the Abe-Ouichi paper hints at the earth system being an injection-locked oscillator to use an electrical analogy. In this context, the delays and heat storage elements inherent to the earth system is driven by an external oscillation of insolation due to variations in eccentricity which excite this particular resonant mode inherent to the earth system. Just as an electrical oscillator has its amplitude of oscillation hard-limited by the battery, so also is the temperature oscillation limited by the amplitude of external insolation changes? This is a non-linear system but one can still get reasonable insights with linear analysis. Details of whether warming and cooling occur at different rates would then be simply mechanisms equivalent to differences in pull-up and pull-down strengths (the rising versus falling edge rates) in the electrical analogy. But then to say that Milankovitch cycles are not the dominant cause of glacial cycles would perhaps be equivalent to saying that noise can excite a characteristic frequency for the earth system.
Of course I forgot perhaps the most important problem with Lubos Motl’s argument: thanks to the anthropic principle, any argument against “fine-tuning” of observed parameters which if set otherwise would have prevented our existence fails. That is, if your argument is:
* f close to 1 is impossible because that means with high probability once in a while f would be > 1 and
* f > 1 implies within a short period of time Earth would be uninhabitable and we wouldn’t exist
* but we do exist, so therefore f cannot be close to 1
Then the argument fails because the last part of it is an absolute, not optional – we DO exist, that’s why we’re even making observations and arguments like this. So no matter the unlikelihood involved in f being close to 1 and never exceeding it up to this point in time, if the alternative is our not existing, then the likelihood of it has no bearing on what actually happened.
Ice age climate instability could be part of the reason we are here at all, as intelligent observers of the universe – near-unstable or actually unstable climate could be a prerequisite for evolutionary selection of intelligent forms of life…
Arthur,
Yes, I think many people use the anthropic principle the wrong way around. As I understand it, the simplest form would be to ask the question “why does the universe/our planet have the properties that it has?” and the answer would be “if it didn’t, we wouldn’t be here to ask the question”.
Reading those SoD posts on the ice sheets can be a little confusing, mainly because he focused on the (necessarily confusing-seeming) ~ 40-year process of trying to understand the cycles rather than its recent conclusion, to the point that he was about to strike out into harmonic oscillation territory before I noted that he had missed something important.
Here’s a public copy of Abe-Ouchi et al. (2013).
As a non-specialist, the crutch I use to assess something like this is to wait a little while and see how the field reacts to it, noting that there are some very smart people (Peter Huybers e.g.) who publish on the topic. As I pointed out at SoD, subsequent literature and conference activity show subsequent embellishment of the idea but zero push-back. That plus my sense of the major pieces of the puzzle having fallen neatly into place settles things as far as I’m concerned.
Pekka: “Basically the phase of glaciation ends when it has persisted for long enough, not when the Milankovitch eccentricity cycle forces it to end.”
I think that’s not quite right. Eccentricity *is* the key factor in initiation of the terminations, albeit not in a straightforward way:
BTW, Nobodyknows, let’s be clear about the role of CO2: It’s just a gas, and if we see a short-term increase of it one thing we can know is that *something else* acted to make that happen, and it’s pretty much certain that the something else has to be a warming somewhere in the climate system. So the denialist argument about the timing of warming vs. CO2 increase as reflected in the Antarctic ice cores is and has always been a red herring. It *is* hard to tease the timing of those factors out of that record, but that makes sense given that the deglacial process was driven from North America.
Steve,
I know very well that eccentricity modulates the precession signal (that has been discussed in length at SoD and I have also commented on that). That by itself does not tell, how powerful that signal is in forcing glaciation or deglaciation.
Yes. I couldn’t really understand why Pekka said that SB’s understanding of this paper was the same as his *because* SB (and me) see ice sheet dynamics (size; volume; latitudinal extent) being engaged by orbital forcing once the Laurentide exceeds a certain threshold for these factors.
RB, it’s much more complicated than that. Bear in mind that the present ice age only became possible when the balance of tectonic processes (volcanism vs. weathering) resulted in CO2 levels dropping, and is a rarity in the largely glaciation-free last few hundred million years. It will end in another few million years as the supercontinent cycle reverses and CO2 once again rises. The present anthropogenic disruption of the climate cycle is a temporary blip since any excess CO2 we produce will be sequestered with 100,000 years or so.
Pekka: “That by itself does not tell, how powerful that signal is in forcing glaciation or deglaciation.”
Maybe I’m unclear as to the point you’re making, but Abe-Ouchi et al. modeled that.
Just to add, RB, Milankovitch cycles operate on climate constantly, but can only modulate glaciers if CO2 levels are low enough for there to be glaciers to modulate.
Steve,
The influence of the eccentricity cycle is to lead to a very smooth alternation of weaker and stronger precession cycles. Averaging over the full precession cycle the linear effects cancel, while some nonlinear effects remain. Those nonlinear effects are modulated by the eccentricity cycle. (The obliquity cycle makes the reality even more complex, but the idea should be clear).
The glacial cycle has a highly non-sinusoidal form that consists of long period of glaciation and a much shorter period of deglaciation. The glacial cycle has also varied in length. Only a few most resents cycles have had a length similar to the eccentricity cycle, but even those lengths have varied.
How different factors combine in creating the glacial cycle, what’s the role of Milankovitch cycles and what that of the state of the Earth system at the point of time, is surely a complex question (your answer to RB seems to tell that you agree on that). To me it seems plausible that the state of the Earth system has the largest influence, and the Milankovitch cycles a smaller one, the alternative is that the relative importance is reversed. I would expect that most agree that both have some role (again your answer seems to tell that you agree). Specialists understand certainly much more on all that, but my impression is that there’s still a lot to explain before the issues can be considered well understood.
Since this post was really meant to be a critique of David Wasdell’s document, I thought I might summarise what I think the general views are (I have found the discussion on feedbacks and glacial cycles very interesting though).
That’s my sense of the general view, but if others have other thoughts, feel free to add them.
Pekka, AFAICT our only real disagreement is about the extent to which this stuff has been pinned down, but that’s really not worth pursuing further.
How about posting on the Mora et al. kerfuffle, Anders?
Steve,
I’m not quite sure what to make of the Mora et al. kerfuffle. As I understand it at the moment, Mora et al. produced an overly precise result that rather ignored earlier work. I shall have to do a bit of reading, I think.
This is the “theory” and the “expert” you are promoting:
“Mathematical Derivation:
Radiative Damping Coefficient = 3.8wm-2 C-1
1°C increase in surface temperature compensates for
3.8 watts per square metre decrease in radiation
Radiative change for increase of 5°C, (Ice-age
minimum to Pre-Industrial Benchmark)
= 19.0wm-2
CO2 contribution = 2.36wm-2
hence Amplification Factor = 8.0
Temperature change for double CO2 alone = .97°C
so Sensitivity = 7.8 C ”
As I understand the theory: According to this “expert” there are one forcing agent, CO2, and several feedback mechanisms that caused the melting of ice age. CO2 is the ultimate melting agent, and is nearly 100% responsible for what happened.
nobodyknows,
Except that this “expert” is wrong, and that is one of the points that people have been making in the comments. Just because someone writes a document, doesn’t mean you have to believe it. Be more skeptical!
nobodyknows
I seem to recall mentioning not so long ago that CO2 and CH4 are feedbacks to orbital forcing.
It would be nice not to have to repeat myself for a third time. Perhaps you would now do as I suggested earlier and read around the topic? Posting ignorant rubbish on the internet is not helping you or anyone else here.
Try this: Shakun et al. (2012) Global warming preceded by increasing carbon dioxide concentrations during the last deglaciation
A temperature increase of 5C from 283C to 288C between glacials/interglacials requires 27W/sq.m by the S-B law not 19W/sq.m.
chipster07,
There’s an emissivity factor that you need to consider. An increase in radiative forcing of around 3.7W/m^2 (at the top of the atmosphere) produces an increase in surface temperature of 1 degree. Therefore an increase of 19W/m^2 increases surface temperatures by 5 degrees.
@ATTP: An increase in radiative forcing of around 3.7W/m^2 (at the top of the atmosphere) produces an increase in surface temperature of 1 degree.
Under what assumptions? That ΔRF = 3.7 W/m2 initially and decreases as T, initially at T0, approaches T0 + 1? And that the surface heat capacity is negligible so that equilibrium is reached almost immediately?
If so then this doesn’t seem terribly applicable to a situation with feedbacks, nor to a planet with oceans.
If not then it would helpful to know how to interpret 3.7 W/m2 in the light of the assumptions.
Hopefully there’s an answer that can avoid falling back on computer models. Otherwise I’d say “And then there’s computers.”
I’m on holiday so don’t have a calculator to hand (and am commenting on a tablet) but I think you can just consider the greenhouse effect in reverse. Surface temperature of 288 K ends up producing an outgoing flux of a 255 K body. If you use that to determine how much the outgoing flux would change if surface temperature changes by 1 K I think you get around 3.7 Wm^-2. Conversely an increase in radiative forcing would, by itself, increase the surface temperature by 1 K.
@ATTP: I’m on holiday so don’t have a calculator to hand (and am commenting on a tablet)
I thought all tablets had calculators these days. 🙂
@ATTP: If you use that to determine how much the outgoing flux would change if surface temperature changes by 1 K I think you get around 3.7 Wm^-2.
I’ll take that as a “yes” to my question, “Under what assumptions? That ΔRF = 3.7 W/m2 initially and decreases as T, initially at T0, approaches T0 + 1? And that the surface heat capacity is negligible so that equilibrium is reached almost immediately?”
In that case my point is that “this doesn’t seem terribly applicable to a situation with feedbacks, nor to a planet with oceans”, such as entailed by chipster07’s “between glacials/interglacials”.
But even without feedbacks, merely applying SB arguably over-simplifies things, as can be seen for example from the 377 comments back in 2010 at the early days of CE. Like the parson’s egg, that thread was good in spots (my explanation on Dec.13 of Venus’s 740K temperature was completely wrong for example), but it would be a pity not to extract and condense the good parts.
In any event I have difficulty seeing what bearing no-feedback sensitivity has on paleoclimate.
@And Then There’s Physics
What emissivity are you applying? I don’t think emissivity has anything to do with it as far as I can see. The reason why you have calculated a 5C temperature change from a radiative forcing of 19W/sq.m is because you applied it to the TOA at a temperature of 255C and I applied it to the surface at a temperature of 283C (5C lower than the average surface temperature of 288C, which I believed to be a reasonable approximation for the average surface temperature during a glacial). I actually calculated an increase of 4.9C on a baseline temperature of 255C, which is close enough to 5C. However I don’t see how applying a 19W/sq.m of radiative forcing would produce 5C of global warming because to get a temperature increase of 5C at a surface temperature of 283C requires 27W/sq.m. Also a radiative forcing at the TOA would not necessarily produce a corresponding increase at the surface because of the way the land and ocean absorb radiation differentially. Because water covers 70% of the surface and has such a high latent heat of vaporisation a large portion of the downward radiation impinging on the surface would be absorbed in the production of water vapour without raising the surface temperature at all.
@Vaughan Pratt “Under what assumptions?”
A straightforward application of the Stefan-Boltzmann law. The Stefan-Boltzmann law is a well-established universal law of physics and there is no circumstance in which it does not apply. It applies to all bodies that absorb and emit radiation and while it strictly applies to blackbodies it can be generalised to cover grey-bodies when combined with the absorptivity/emissivity of the body in question. I took a look at your comment where you said “Venus’s atmosphere contains about as much carbon as the whole of Earth, yet that’s only enough to get it up something like 500 K, I forget the precise number. It reaches its surface temperature of 740 K by using only trace amounts of carbon monoxide (a strongly absorbing greenhouse despite being diatomic”. Venus actually has 157,000 times the mass of CO2 than Earth. The mass of Venus’s atmosphere is 4.8×10^20kg and the CO2 concentration on Venus is 96.5% (around 4.7×10^20kg). But the mass of the atmosphere on Earth is 5.1×10^18kg and that has a CO2 concentration of 0.039% (around 3×10^15kg) (corrected for molecular weight). I think a common mistake is assuming that because both planets have the same percentage of CO2 then that must mean they have the same amount of CO2, without taking into account the fact that Venus has a far denser atmosphere than Earth.
VP,
Bear in mind that this post was a critique of someone else’s work where the general conclusion was that it was indeed far too simple. However, I think it is still roughly correct that if surface temperatures rise by 5 degrees then that implies a total change in radiative forcing (external forcings plus feedbacks) of around 19Wm-2. It may be simple, but it’s probably still a reasonable estimate.
chipster07,
A few things. This isn’t my calculation. Someone asked me to post this so it could be critiqued by others, almost all of whom agree that it is too simple a calculation.
Let’s clarify a few things though,
Again, it wasn’t me, but, a forcing is defined (unless I’m mistaken) as a change in TOA flux. So, a net change (let’s say an increase) in radiative forcing of 19Wm-2 means that if nothing else were to change the outgoing flux would be 19 Wm-2 less than the incoming flux (we’d be gaining 19 J per second per square metre). To return to radiative balance would require an increase in temperature of about 5 degrees. You are, however, correct that a 5 degree increase in surface temperature would produce a 27Wm-2 flux from the surface, but it would only produce about a 19 Wm-2 increase in TOA flux (energy is returned to the surface so as to conserve energy).
The emissivity I’m talking about is the surface emissivity which you can get from the following
You could use 283 K instead of 288 K if you wanted to but one way to consider the greenhouse effect is that only about 60% of the surface flux escapes through the atmosphere.
I’m also a little surprised that this is at controversial as one of the things that I thought everyone accepted was that a change in forcing of 3.7Wm-2 would produce (by itself) an increase in surface temperature of just over 1 degree.
ATTP,
Calling that value 0.61 surface emissivity is surely not a very common practice, and may be rather confusing. You are net the only one to apply that practice, but to me it’s too confusing.
The value 0.61 is the surface emissivity, when the atmosphere is considered a coating that forms part of the surface, but is not included in the determination of the surface temperature. In that view the whole atmosphere is a selective coating that makes absorptivity of solar radiation 0.70 and emissivity of IR 0.61.
“I’m also a little surprised that this is at controversial as one of the things that I thought everyone accepted was that a change in forcing of 3.7Wm-2 would produce (by itself) an increase in surface temperature of just over 1 degree”.
No need to be surprised my friend. I agree that 3.7W/sq.m would give us a 1C temperature change in the atmosphere and that’s accepted by both sides of the debate, although to increase the surface temperature by 1C would require 5.5W/sq.m of radiance according to the Stefan-Boltzmann law by my understanding. The 1C change in surface temperature is actually calculated a little differently than just applying the Stefan-Boltzmann law. According to Trenberth the total greenhouse back-radiation from all sources amounts to 333W/sq.m and the total solar radiation absorbed by the surface is 161W/sq.m which equals 231k. Taking away ~80W/sq.m from evapotranspiration gives us 194K. But the actual surface temperature is 288K which is a difference of 94C. Therefore that gives us a linear relationship between W/sq.m and K of 0.282C per 1W/sq.m. So a radiative forcing of 3.7W/sq.m would give us 1C of global warming. That’s where the 1C of global warming from 3.7W/sq.m comes from, rather than applying the Stefan-Boltzmann to the surface, which is personally what I would find more appropriate, but hey-ho.
To get 0.282C per 1W/sq.m just divide 94K by 333W/sq.m in case I didn’t make that clear.
Chipster,
The Stefan-Boltzmann law can be applied to the radiation to space. When that’s done it gives by definition the relationship between OLR intensity and the effective radiative temperature ERT) of the Earth. ERT is not a temperature of any specific location, neither it’s an average temperature of any volume or surface, it’s just what’s obtained by inverting the Stefan-Boltzmann formula.
Next we can ask, how various average temperatures changes relative to the change of ERT. It turns out that both the average surface temperature and the average temperature at a fixed height in the troposphere are likely to change approximately equally and also approximately as much as EST, because the average lapse rate does not change rapidly, and because such an nearly uniform change in temperature over all altitudes of the troposphere changes also ERT by approximately the same amount.
When temperatures changes approximately equally at all altitudes, the power of emission changes more at low altitudes and at the surface. That does not lead to contradiction, because the change in upwelling radiation is to a large part compensated by the change in downwelling radiation. What’s left after this partial cancellation is balanced by a change in convective heat transfer (which includes also latent heat transfer). For this reason the power of emission from the surface is not as significant as OLR.
Not sure what it is that you’re specifically trying to communicate to me here Pekka.
Chipster,
It was a reaction to your words:
and an attempt to explain, why I don’t consider it particularly essential to apply the S-F law to the surface.
Hansen & Sato (2012) estimates s_ff empirically from the LGM/Holocene transition (section 3.2; emphasis added):
chipster07 is playing the obvious and long-repeated game. “Both sides would agree” indeed. From his POV, agreeing to 1.1C and then arguing about the feedbacks leading to ~3C fast sensitivity is great since many not paying attention to or not understanding the details will think that 1.1C is a best case and 3C is a worst case, having been trained to think that the truth must exist between two defined sides. A parallel discussion is common with respect to 3C (which note can never happen in the real world since slow feedbacks kick in too soon) vs. the real-world (Earth system) sensitivity of ~5-6C, although people on chipster07′ “side” dislike that one so much that they seem to prefer to not have it at all, preferring to lather, rinse, repeat with the 1.1C. It’s politics at work, not physics.
chipster07,
I’m rather confused by your response. As Steve B. suggests, you seem to be both agreeing and disagreeing. An increase in surface temperature of about 1 degree (maybe 1.1 or 1.2, but that’s not that important) is associated with a change in radiative forcing of about 3.7 Wm-2. Therefore, an increase of 5 degrees would be associated with an increase in radiative forcing of about 19 Wm-2. I don’t think this is remotely controversial.
BBD,
Your comment seems broadly consistent. Climate sensitivity of 0.75 degrees per Wm-2 means a 5 degree change in surface temperature is associated with a change in external forcing of 6.66 Wm-2. A feedback amplification factor of 2.5 then gives an overall change of around 17 Wm-2.
That isn’t really all that relevant to this post though. I think we’ve already established that what is proposed in the document has already been done more thoroughly.
Righto Pekka, thanks for that. I understand the process of determining Earth’s effective blackbody tempeature with the S-B law and have done it myself. But I still don’t see how applying a specific RF to the atmosphere would yield exactly the same temperature increase at the surface – they have two different baseline temperatures and the S-B law implies that as a temperature of a body increases it requires increasingly higher increments of RF to produce the same temperature increase in accordance with the 4th-root relationship between temperature and radiation-intensity regardless if “the average temperature at a fixed height in the troposphere is likely to change approximately equally to EST”. The S-B law implies that a RF of 3.7W/sq.m is only sufficient to increase the temperature of a body 0.7C when the temperature of that body is 288K. And Steve, I was just pointing out that as far as I can tell it’s acknowedged by skeptics and the IPCC that doubling atmospheric CO2 would lead to around 1C of warming, I don’t see how that is me “playing a game”. But whatever, think what you like.
I think it depends on what the baseline temperature is ATTP. I agree that the S-B law would give about 1C (I calculated 0.7C and that is not really a big disparity) at the surface but disagree with the contention that 19W/sq.m would increase surface temperature by 5C from 283K to 288K between glacials and interglacials. The S-B law would require a total energy input of 27W/sq.m on a baseline temperature of 283K for the body to rise by 5C. 27W/sq.m. Not 19W/sq.m.
That’s just ludicrous. Doubling CO2 *cannot* lead to any such thing on this planet, other than as a point that will be passed through on the way to something much higher.
So can we say instead:
“It’s acknowledged by skeptics and the IPCC that doubling atmospheric CO2 would lead to around 5-6C of warming.”
That would be a true statement, except for the small detail that (pseudo)skeptics (aka deniers) wouldn’t agree with it. Real skeptics tend to be more worried that the IPCC has it wrong on the low side.
Or we could say:
“It’s acknowedged by some pseudoskeptics (let’s not forget e.g. the Sky Dragons) and the IPCC that doubling atmospheric CO2 on an otherwise Earth-like planet with no water (and thus no biological feedbacks as well) would lead to around 1C of warming.”
Yes, we have achieved consensus! But tell me, why do you like to elide the bit about no water?
Ferrgoodnessake Steve we are talking about the effects of CO2 alone without the feedbacks. On a side-note I do realise that the figure of 27W/sq.m is calculated with an emissivity of 1.0. What emissivity are you guys working with? 0.7?
chipster07
~1C for 2xCO2 is the no feedbacks response. There’s a bit more to it than that.
chipster07
We crossed there.
I know that the 1C from x2-CO2 excludes the feedbacks. I just said and apparently everyone apart from Steve understands that we are talking about CO2 only!
Notice how chipster07 is conflating the RF of a 1C increase with sensitivity to doubled CO2.
chipster07
I think the problem may be that your S-B calculation omits a correction for albedo.
[Mod: Be nice, please]
*You* are talking about CO2-only, chipster07. How is that useful or relevant out of context? Do you just like to repeat that 1C sensitivity figure a lot? Try reading the post again. The CO2-only sensitivity is only significant as something to subtract to derive the overall feedback, which note has components that can’t be easily calculated from measurements or first principles.
Just to note that in sensitivity calculations based on (near-)equilibrium paleoclimates like the LGM, if the CO2-only response gets reduced the feedbacks must increase correspondingly. Which feedback(s) do you think should be increased based on your downward adjustment, chipster07?
Chipster,
There’s a near radiative balance at TOA, and that radiative balance controls the effective radiative temperature of the Earth.
At surface there’s a strong radiative imbalance (absorbed solar SW + downwelling IR add up to a much higher flux than the emission from the surface). A strong imbalance does not control the surface temperature. The surface temperature is controlled by the balance that’s formed, when convection of sensible heat and latent heat are included. The convective processes limit the temperature difference between the surface and the upper troposphere to the value that corresponds to the environmental lapse rate of about 6.5 C/km. Thus the surface temperature is not fixed by the radiative energy balance at the surface but by the radiative energy balance at TOA in combination with the nearly constant average lapse rate.
@chipster07 (to me): I took a look at your comment where you said “Venus’s atmosphere contains about as much carbon as the whole of Earth, yet that’s only enough to get it up something like 500 K, I forget the precise number. It reaches its surface temperature of 740 K by using only trace amounts of carbon monoxide (a strongly absorbing greenhouse despite being diatomic”.
That was my understanding in 2010, based on an overly simplistic application of the Arrhenius logarithmic law. Subsequently I considered the physics more carefully and realized that the law was not applicable to Venus at all. Instead the surface temperature on Venus is determined by the lapse rate of the Venusian atmosphere, which despite the obvious huge differences from Earth’s atmosphere is remarkably close to that of Earth.
Using this reproduction of Jenkins et al’s plot of Venus’s temperature profile (the original is behind a paywall), a line from 78 km on the altitude axis to 740K on the temperature axis fits the profile very well and corresponds to an observed lapse rate (assumed constant) of (740 − 100)/78 = 8.2K/km (observed by both Russian and US landers). This is only slightly less than the theoretical value of 8.8K/km given by the formula g/c_p at the Wikipedia article on lapse rate using g = 8.87 m/sec2 and c_p = 1.01 at p = 10 bar, T = 200 °C using this CO2 calculator.
Venus radiates its heat to space from the top of the atmosphere, roughly 70-90 km. One might assume that this is because CO2 is a greenhouse gas, and that if it were replaced by an equivalent quantity of a non-GHG such as nitrogen the radiation would instead be from the surface. However this reasoning overlooks the fact that the top 25 km of Venus’s atmosphere is a cloud of concentrated sulfuric acid droplets and sulfur dioxide, which gives Venus its albedo of 0.9 (i.e. reflecting shortwave radiation) as well as radiating all its outgoing longwave radiation (OLR) to space. Hence the OLR from Venus will be from the clouds independently of whether the atmosphere below is a GHG.
Nevertheless replacing Venus’s CO2 atmosphere with nitrogen will have an effect, namely to turn it from opaque (at IR wavelengths) to transparent, thereby permitting the 17 KW/m2 radiation from the surface (at 740K) to heat the clouds directly instead heating the bottom of the atmosphere, raising their temperature from 450K (at the bottom of the haze at 30 km, below the main clouds) to more than 700K. This would in turn add some 250K to the whole cloud layer, greatly increasing OLR, which in turn would greatly reduce the temperature of the whole atmosphere and that of the surface (Planck feedback).
Conclusion: Venus’s GHG atmosphere does play a major role in keeping the surface of Venus hot, though the mechanism is not as simple as one might think, depending among other things on the thickness of the cloud layer at 50-75 km and the haze layer at 30-50 km.
As you can see from what I wrote in 2010, my understanding has changed greatly in the intervening four years.
Saying somebody is “off their head” isn’t allowed on this site. Damn. That sort of thing is thrown about all the time on WUWT. Look Steve, I really don’t see why you’re getting so up-tight about me discussing the CO2-only RF, it’s all rather weird. It was simply in response to ATTP’s post on the 22nd at 3:13. Besides the positive feedbacks responsible for increasing the surface temperature to ~3C are unproven to my mind so why would I discuss them? You say that if the CO2-response decreased then the feedbacks must increase, but that seems false to me. Rather I think that the positive feedbacks are very small or either non-existant and that the RF from the Milankovitch-cycle has been grossly underestimated. Nice talking to you Steve.
But Milankovitch / orbital forcing barely alters total global insolation. It just moves it around, seasonally and spatially.
So positive feedbacks are required for orbitally-triggered deglaciation.
@ATTP: However, I think it is still roughly correct that if surface temperatures rise by 5 degrees then that implies a total change in radiative forcing (external forcings plus feedbacks) of around 19Wm-2. It may be simple, but it’s probably still a reasonable estimate.
(Let’s assume for now that the oceans are 10m deep so that we can ignore the impact of their heat capacity on these calculations.)
The following is very much in line with what Pekka wrote at July 24, 2014 at 12:38 pm (some 20 or so comments earlier).
I would say part of the problem in this discussion is the lack of a clear before-and-after picture. Here’s my attempt at one. If anyone feels they have a better one please propose it and we can compare pictures.
My picture for each of before and after raising the surface temperature 1K gives the temperature in Kelvin at three altitudes, 0 (surface), A, and B, in that order. I’ll assume a spherical surface (no mountains) at a uniform temperature (same at all latitudes) of 288K before (and hence 289K after). I’ll also assume that Earth’s effective temperature is 255K (based on a solar constant of 1367.6 W/m2 and albedo of 0.7). I’ll also assume a constant lapse rate throughout the atmosphere, independent of both surface temperature and altitude.
Here’s my Before-and-After picture, in degrees K for the three altitudes.
Before: 288 255 254
After : 289 256 255
I’ll define the effective OLR photosphere to be the altitude at which the temperature is Earth’s effective temperature, namely 255K. This is at altitude A before and at altitude B after. In practice OLR originates from a continuum of altitudes; here I’m assuming for simplicity that it originates at a single altitude, i.e. a lumped model.
If we further assume a lapse rate of 10K/km, altitude A must be at (288 − 255)/10 = 3.3 km and similarly altitude B at 3.4 km.
If your picture is nothing like this then I would like to understand what it is and why it’s better.
If and when we agree on a picture I’ll then feel comfortable talking about equilibrium sensitivity without feedbacks and with. Otherwise I worry that we’ll be talking at cross purposes.
VP,
I actually think what I’m saying is much simpler than you seem to think. I’ll try to explain one more time. Imagine everything stays fixed apart from the surface temperature that increases by 1 degree, then the outgoing flux will increase by 3.7 Wm-2. Do you agree with that?
Consequently, if there is an increase in radiative forcing of 3.7 Wm-2 (could be the Sun, could be GHGs, could be …..) the surface temperature would need to increase by 1 degree to return to energy balance (ignoring feedbacks for the moment).
Therefore if there is a change in surface temperature of 5 degrees, that must be associated with a total change in radiative forcing (external forcings plus feedbacks) of about 19 Wm-2 (It’s probably more like 17 Wm-2).
I agree with your picture. What I’m saying is not inconsistent. I think, in fact, you can actually get the same answer from your picture. Consider the altitude that was initially 255 K (i.e., the emission altitidue). A 1 degree increase in surface temperature increases the temperature at that altitude to 256 K. The change in flux at that altitude is therefore
Which is the same as what I’m suggesting. An increase in surface temperature of 1 degree, without changing anything else, increases the outgoing flux by 3.7 Wm-2.
I agree with the above comment of ATTP (this latest formulation is perhaps the clearest in this thread).
I add one more point on the separate question, whether it makes sense to say that the surface emissivity of the Earth as seen from space is 0.61 for LWIR. Actually it doesn’t really as that value does not satisfy Kirchhoff’s law that tells that absorptivity is equal to emissivity for given wavelength. The absorptivity of the Earth is close to 1.0 for LWIR. Thus 0.61 cannot be emissivity.
@ATTP: [If] everything stays fixed apart from the surface temperature that increases by 1 degree, then the outgoing flux will increase by 3.7 Wm-2.
That’s certainly true of an airless planet with a surface temperature of 253.6K and unit surface emissivity. It is as you say very simple as it makes use only of SB.
For a planet with a greenhouse atmosphere, with “outgoing flux” referring to OLR at TOA, and a surface temperature of 288K, if the surface emissivity were 0.683 then surface radiation would indeed increase by 3.7 W/m2, again by SB.
Are you claiming the OLR will also increase by 3.7 W/m2? And if so by what calculation or reasoning? How do you deal with the fact that GHGs are trapping some of the surface radiation?
@ATTP: Which is the same as what I’m suggesting. An increase in surface temperature of 1 degree, without changing anything else, increases the outgoing flux by 3.7 Wm-2.
It doesn’t look the same to me. I assumed an initial surface temperature of 288K. What you’re suggesting would be true of the surface radiation if and only if the surface emissivity is 0.683. Furthermore the increase in OLR in my picture is zero, not 3.7 W/m2. And moreover I don’t see how you obtain 3.7 W/m2 for OLR, unless by “outging flux” you were referring to flux from the surface.
Maybe these inconsistencies I’m encountering are merely the result of some misunderstanding I’m having, or conflicting terminology, but in any event I’ll be very grateful when they’re straightened out.
@Pekka: I add one more point on the separate question, whether it makes sense to say that the surface emissivity of the Earth as seen from space is 0.61 for LWIR.
I agree that it should be 1.0, Pekka, for the reason you give. However in the comment I responded to, ATTP said nothing about emissivity. Should I have assumed it was implicit in what he said? Presumably not, since one would need a specific value to incorporate it into the maths.
I presume your 0.61 for the emissivity comes from assuming a surface temperature of 300K or 27 °C (80 °F). Isn’t that rather hot?
Chipster,
I the reason people get frustrated by folk quoting a 1degree no feedback as being some sort of real figure is because it is used as a rhetorical device.
Thing is, the “no feedback” figure depends on a model. The model assumes (amongst other things) constant water vapour in the atmosphere regardless of temperature. That’s clearly unphysical.
A reasonable physical assumption is constant relative humidity as temperature changes. That gives a feedback equating to about three degrees/doubling.
You can add in other feedbacks if you want; some are negative, some positive, but all small relative to water vapour.
Saying that you “think that the positive feedbacks are very small or either non-existant [sic]” is unlikely to convince anyone; it’s just your opinion and is contrary to all research.
If you’d like to understand why relative humidity is fairly constant, try this:
http://www.gfdl.noaa.gov/blog/isaac-held/2014/06/26/47-relative-humidity-over-the-oceans/
@ATTP: without changing anything else,
Perhaps this phrase is the problem. I have no idea what it means.. If I pull your chair out from under you without changing anything else, do you fall to the ground or remain suspended in the air?
VP,
All I mean is that the only change is an increase in surface temperature. As you yourself illustrate in your comment, if the lapse rate is unchanged, then that would lead to an increase of 1 degree at all altitudes. Given that this won’t change the effective emission height (which I agree is much more complex than being a single height, but it’s okay to think of it that way for this illustration) that means an increase in outgoing flux of 3.7 Wm-2.
Similarly, if you consider the definition of a radiative forcing it is defined as
So, it is some external effect that changes the radiative balance so that there is either more energy coming in than leaving or more going out than coming in. It’s defined simply in terms of how it would effect the energy balance if it was the only effect operating. In reality, it can’t operate in isolation, but it is still possible to determine the effect it would have were this possible.
One issue with this whole discussion about 5 degrees being associated with a change in radiative forcing of 19 Wm-2 is that it somewhat violates the definition of a forcing. A forcing is – as suggested above – associated only with external factors (anthropogenic emissions, volcanoes, Sun) while the amplification of this is through feedbacks. The 19Wm-2 is therefore both forcings and feedbacks, but it is still roughly the right quantity, even if it is not strictly all a forcing.
ATTP: Given that this won’t change the effective emission height
Why not? I wrote
I’ll define the effective OLR photosphere to be the altitude at which the temperature is Earth’s effective temperature, namely 255K. This is at altitude A before and at altitude B after.
What I meant by this was that the effective emission height changed from A to B.
Perhaps what you meant by “without changing anything else” included not changing the effective emission height. But that would be like remaining suspended after the chair was pulled out from under you.
VP,
Hold on, in your example you said
If this is because the surface temperature has gone from 288K to 289K then the effective emission height is unchanged. Where it was once 255K, it is now 256K, so the planet is now emitting more energy into space than it was when the surface temperature was 288K (by 3.7 Wm-2). The only way that it can be in balance is if there has been some change in the atmosphere to increase the effective emission height so that it is now at the same altitude as where the temperature is 255K. This change would be something (increase in GHGs) that produces a 3.7 Wm-2 radiative forcing to balance the increase in temperature.
I’m also rather confused about people’s issue with the 0.61 factor. It comes very trivially from this
i.e., the right hand side is the actual outgoing flux, the left-hand side is what fraction of the surface flux essentially is able to escape through the atmosphere. If you solve this, you get
I’ve got to admit that I’m finding this discussion all rather confusing as I thought this was all fairly obvious. I’ll maybe address this again when I’m back from my holiday. Time to go back to the pool now though 🙂
Perhaps the difference is that your version of the Before-After scenario has the After configuration out of equilibrium. If so then we need to talk more about what you consider disequilibrium to be like. Feedbacks in disequilibrium need be nothing like those in equilibrium
VP,
Okay, but then you’ve changed two things. You changed the surface temperature and you’ve changed something in the atmosphere so that the effective emission height is where the effective temperature is 255 K. If – as I was trying to illustrate – you only change the surface temperature then the effective emission height does not change, the temperature there increases by 1 K and the outgoing flux increases by 3.7 Wm-2.
VP,
Yes, that is precisely what I’m suggesting. I’m simply trying to illustrate that a change in surface temperature is associated with a change in radiative forcing of 3.7 Wm-2.
Where it was once 255K, it is now 256K, so the planet is now emitting more energy into space than it was when the surface temperature was 288K (by 3.7 Wm-2). The only way that it can be in balance is if there has been some change in the atmosphere to increase the effective emission height so that it is now at the same altitude as where the temperature is 255K.
This confirms what I just wrote: you’re assuming disequilibrium. My fault, I should have been more explicit that both Before and After in my scenario were in equilibrium. (It was implicit in the move of the effective OLR photosphere from A to B.)
Disequilibrium is more complicated (for me anyway) and I don’t (currently) understand any purportedly simple scenario based on it. Easy for you, difficult for me.
VP,
But a radiative forcing is – by definition – out of equilibrium. That’s the point. If GHGs produce a radiative forcing of 3.7 Wm-2 that means that – alone – they would reduce the outgoing flux by 3.7 Wm-2. If there were no feedbacks, then returning to equilibrium would require an increase in surface temperature of about 1 K. Of course feedbacks do operate and nothing ever operates in isolation, but it is still possible to make these kind of estimates. Anyway, must go back to the pool 🙂
ATTP,
The problem with the surface emissivity starts with the definitions of surface, surface temperature, and emission from the surface.
In the basic case all these are well defined, but in the case of the Earth, the word surface refers normally the interface between the atmosphere and the solid/liquid parts of the Earth. The IR emissivity of that surface is high, only a few percent below 1.0. This is what most people understand by (average) surface emissivity of the Earth. That surface has also a rather well defined temperature at every point of the surface.
The value of 0.61 is not surface emissivity in that sense. It’s the ratio of OLR at an altitude of more than 10 km to the emission of a black body of the temperature of the surface defined as in the previous paragraph. It’s so much less than 1.0, because the temperature of the emitting material is lower than that of the black body used as reference, not because the emissivity is lower. Here the intensity of radiation and the temperature refer to locations more than 10 km apart. The word surface refers to two different things in expressions surface temperature and emission from the surface. Using the word in two different meanings in calculating emissivity leads to confusion – or worse.
There are similarities with the influence of selective coating on a surface that would otherwise have a high emissivity, but there are also essential differences. One of the essential differences is the related absorptivity. For a real surface Kirchhoff’s law is valid, for the multitemperature structure of the Earth with atmosphere it’s not, if the value 0.61 is taken as emissivity.
If you only change the surface temperature then the effective emission height does not change, the temperature there increases by 1 K and the outgoing flux increases by 3.7 Wm-2.
No, if you only change the surface temperature without changing anything else (your wording) then the temperature at the effective emission height does not change.
This is what I meant by not understanding “without changing anything else.” You seem free to choose what to change and what to leave unchanged.
In practice, eventually the temperature at both A and B will increase by 1 K, but it will take quite a long time, during which other things may change. Arbitrary choices of what changes and what doesn’t after some initial change can be arbitrarily unphysical.
@ATTP: But a radiative forcing is – by definition – out of equilibrium.
Yes, perhaps I should have begun by saying that this was what I was proposing to replace by a different picture, one in which both Before and After were in equilibrium, without saying anything about whether or not water vapour or feedbacks were in the picture. Very minimal assumptions.
Defining anything to be a disequilibrium situation while reasoning about it as though it were an equilibrium situation (“without changing anything else”) is unphysical. This is particularly so with radiative forcing, which is never an instantaneous thing (well, except for a megavolcano perhaps with the ash dissipating quickly and the CO2 hanging around much longer).
Saying it is a good back-of-the-envelope estimate is only convincing when you’ve shown that it yields results close to what you’d get from modeling it properly, i.e. not artificially holding one variable stationary while allowing another to vary over a period of years or decades, which is the situation with radiative forcing. The 1 K rise we’re just completing now started in 1910.
The advantage I see for my Before-After picture is that it is an equilibrium-to-equilibrium transition that is no more complicated (in terms of assumptions) than the standard equilibrium-to-disequilibrium transition, yet does not raise questions about the nature of the disequilibrium such as the physicality or otherwise of holding one variable fixed while varying another very slowly.
VP,
Sure, but an equilibrium-to-equilibrium transition is one in which we are in energy balance, so it really tells you nothing of why or how something may have changed. Whatever the consequences of climate change the planet will at some point in the future be in equilibrium (or close enough to regard it as being in equilibrium). It’s the changes we are likely to face in getting there that is the issue, not whether or not we’ll ever retain equilibrium.
Having said that, even in your Before-and-After illustration, it is still the case that the flux at the Before emission height increases by 3.7 Wm-2 when temperatures rise by 1 degree, even though your example assumed equilibrium was retained.
Vaughn Pratt:
1) Ander’s scenario requires the increase of surface temperature by one degree, the restoration of convective equilibrium in the troposphere, but not the restoration of radiative equilibrium. Given that it takes hours to restore convective equilibrium, but decades to restore radiative equilibrium, that is not too unrealistic a scenario to consider.
2) Your scenario assumes to much. Specifically, it assumes that the restoration of radiative equilibrium will be the result of feedbacks, whereas for a simple change in surface temperature with no change in forcing, radiative equilibrium is more likely to be restored (after an excursion whose duration depends on the strenght of climate feedbacks) by surface temperatures returning to their prior values.
Vaughan seems to be right in criticizing the assumption of everything else staying the same as that assumption is not applicable to the problem discussed in the original post and in most comments of this thread.
It’s possible to define the radiative forcing from a sudden increase in CO2 concentration as it’s possibly to imagine, how CO2 could be suddenly added uniformly throughout the atmosphere. Here the cases being compared have different temperatures and have had different temperatures for long. Thus all the fast feedbacks have developed fully. In particular the state of clouds is different and that affects significantly the height of emission of OLR.
We have two real states near equilibrium, trying to define a third one that has the temperature of the glacial maximum but otherwise the atmosphere of today leads only to contradictions. Such a state is too far from realism to offer a meaningful point of comparison.
Pekka,
All I’m trying to illustrate is that a change in radiative forcing of 3.7 Wm2 is – alone – associated with a change in surface temperature of 1 degree. Something I had thought was not in dispute. Somehow it now is and so I shall do something more productive – go for a swim.
Pekka,
As regards your comment about surface emissivity I thought it pretty obvious that I was defining as the ratio of the outgoing flux to the flux of a blackbody with a temperature the same as that of our surface. Hence the equations I used. Any chance you could actually put some effort into understanding what people are trying to say?
Pekka, convective equilibrium can be reestablished in a matter of hours, whereas even rapid feedbacks take weeks to have effect. Further, erecting a shield between ourselves and the Sun for 24 or 48 hours seems sufficient to effect a rapid drop in surface temperature. A large enough mirror in lunar orbit could equally raise GMST on the same time scale. There is no reason to think it would be more disruptive at first than injecting 280 ppmv of CO2 into the atmosphere over the same time period. Holding the Earth sunless long enough to drop the GMST by 5 C (or doubling sunshine to raise it) would be more disruptive, but not more so than injecting 8680 ppmv of CO2 in the atmosphere on the same time scale. If, therefore, we are to hold the difficulty of realistic implementation of an abstract scenario as a bar to analyzing the scenario, we might just as well give up on physics altogether and go home.
“I assumed an initial surface temperature of 288K. What you’re suggesting would be true of the surface radiation if and only if the surface emissivity is 0.683”.
Exactly!
“Conclusion: Venus’s GHG atmosphere does play a major role in keeping the surface of Venus hot, though the mechanism is not as simple as one might think, depending among other things on the thickness of the cloud layer at 50-75 km and the haze layer at 30-50 km”.
Thanks for explaining all that, Vaughan. I don’t doubt that it is far more sophisticated as you say. I have always been of the opinion that the back-radiation from the CO2 greenhouse cannot explain the extraordinarily high temperature of the Venusian surface. I think a more likely explanation for the high temperatures on Venus is pressure. By my understanding the greenhouse effect relies on the atmosphere being relatively transparent to incoming short-wave radiation and relatively opaque to outgoing long-wave radiation. But the Venusian surface is completely covered by a thick, dense cloud layer which is pretty-well opaque to both incoming short-wave and outgoing long-wave radiation alike. Under these circumstances the greenhouse effect cannot operate by definition.
“However this reasoning overlooks the fact that the top 25 km of Venus’s atmosphere is a cloud of concentrated sulphuric acid droplets and sulphur dioxide, which gives Venus its albedo of 0.9 (i.e. reflecting shortwave radiation) as well as radiating all its outgoing long wave radiation (OLR) to space”.
Since at least as far back as 2005 NASA were saying that the albedo of Venus was 0.75 (which always did seem incredibly small to me). Then one day in 2011, without giving any public explanation that I’m aware of, they quietly put it up to 0.90. No doubt this albedo-adjustment by a mere 15% will seem inconsequential to most people but it implies a fundamental revision of the thermodynamics of the Venusian greenhouse with which NASA is so fond of comparing the Earth’s. The revised albedo would imply that Venus’ effective surface temperature is 184K. But the actual surface temperature is closer to 733K (NASA Fact Sheet). So something must increase the surface temperature by 549K. It cannot be the back-radiation from CO2 though. When you apply the IPCC’s logarithmic equation to Venus that only gives us a maximum warming of 46.7K.
“You can add in other feedbacks if you want; some are negative, some positive, but all small relative to water vapour”
It is true that higher temperatures would increase evaporation rates and therefore would increase water vapour. But that lasts only until the water vapour turns into cloud which acts as powerful negative feedback. Some might even argue that increasing water vapour is a negative feedback in itself since it actually reduces day-time temperatures (compare the Sahara desert to the Amazon). There is evidence showing that atmospheric water vapour has decreased. Google ‘NASA satellite data shows a decline in water vapour’.
ATTP,
I have understood all the time, what you have called emissivity. What I have argued is that you should not call that emissivity, when it is not.
I wrote my first comment on that in this thread, when I noticed that some others got really confused from your use of the word emissivity.
Pekka,
I agree. I used the wrong terminology.
Tom Curtis,
Yes, the last sentence of your comment was something that I had also considered saying.
Wrong.
Muddled and misleading. Let’s compare them at night. Then let’s average over the year.
Debunked denialist misrepresentation.
If you rely on misinformers, you will remain wrong and confused.
Not this nonsense again. Goddard was wrong, chipster07. Read the link and you will understand why.
Oooh! A conspiracy theory: ‘NASA is covering up fatal flaws in climate theory’. And a reference supporting this claim would be nice. I like my conspiracist ideation fully linked.
Oh, and you skipped right over this:
But Milankovitch / orbital forcing barely alters total global insolation. It just moves it around, seasonally and spatially.
So positive feedbacks are required for orbitally-triggered deglaciation.
Your stuff about negative feedbacks is wrong but you didn’t even acknowledge the correction. I hate it when people do that. It is discourteous and makes me wonder if perhaps they are not acting in good faith.
Chipster,
There are two different definitions of albedo. You can find out that Wikipedia presents the value of 0.9 for the Bond albedo and 0.67 for the geometric albedo taking the values from this paper of Mallama et al (2006)
That you have seen two so different values must be due to the existence of two definitions. The Bond albedo is the one relevant for the energy balance, while the geometric albedo determines the brightness of “full Venus”.
Pressure alone does not lead to the high surface temperature of Venus, but vertical convection does produce the approximately constant lapse rate, and through that a high surface temperature, when the basic properties of the atmosphere are as they are for Venus. The most important properties are the total mass and the altitude and temperature of the layer that dominates in the overall energy balance (like -30C at 65km).
As far as I have understood correctly, the convection that maintains the temperature gradient of Venus is driven mainly by heating of the atmosphere rather than the equatorial surface as it’s on the Earth. What drives the circulation is, however, not essential for the temperature gradient as long as something has the free energy to drive it.
(Working backwards through the comments of the last few hours.)
@Pekka: What drives the circulation is, however, not essential for the temperature gradient as long as something has the free energy to drive it.
Exactly. Moreover none of the energy need be radiative. Much less than 1% of Venus’s strong winds would suffice to maintain the expected lapse rate. You would have to have impossibly still air before the lapse rate could decrease on account of diffusion overcoming convection.
Vaughan,
Maintaining the convection consumes a significant amount of free energy. Thus also the source of the free energy must be rather strong, and the only alternative I can imagine for that is essentially the radiative GHE. What’s needed is a situation, where something tries to force the temperature gradient to exceed the adiabatic lapse rate, and GHE is really needed for that. It’s, however, possible that the driving temperature difference is created at an altitude far above the surface.
Chipster,
“But that lasts only until the water vapour turns into cloud which acts as powerful negative feedback”
Seriously chip, think about it. If the air is warmer, even with cloud formation, there is still more water vapour.
And cloud feedbacks are most likely net positive, although there is uncertainty on that, and it differes according to time of day and altitude of clouds.
I’m done with attempting to engage; you’re clearly set on repeating talking points rather than thinking.
“Wrong.”
Really? I suppose you’ll enlighten me BBD.
“Let’s compare them at night. Then let’s average over the year.”
Did you compare them? I can’t find any definitive averages of their temperatures. Maybe you can.
“Oooh! A conspiracy theory: ‘NASA is covering up fatal flaws in climate theory”.
What a fertile imagination you have. Sorry, it’s not my conspiracy theory. It’s yours that you have projected onto me.
“But Milankovitch / orbital forcing barely alters total global insolation. It just moves it around, seasonally and spatially”.
Based on what? Paleo-climate data? How exactly has the RF from the MC been derived? The hypothesis that positive feedback was the main cause of the Earth’s climate switching between glacial and inter-glacial states is one that sounds reasonable to me on the face of it when I first heard it years ago, although I have seen nothing as yet to convince me that it definitely was the main cause. We know next to nothing about what the Sun was doing at these times and we also know very little too about how the whole climate system was constituted then either. I strongly suspect that empirical measurements of the RF from the MC are impossible without a two-way time machine, but I gather that the assumed globally-averaged RF from the MC according to the IPCC is ~0.7W/sq.m. However since MC theoretically produce smooth sinusoidal changes in solar irradiance I have no idea what discrete step of 0.7W/sqw.m represented, i.e. between which points on which cycle was it measured? My reasons for thinking that the feedbacks are small or non-existent is based on a number of things that would take too long to explain here, i.e. there are hundreds of papers out there showing a very small climate sensitivity, most of which are periodically posted on sites such as WUWT and Jo Nova, although I gather that you think they’re ‘denier websites’.
“Seriously chip, think about it. If the air is warmer, even with cloud formation, there is still more water vapour”.
And there are more clouds too. Clouds act as negative feedback by reflecting incoming solar radiation back-out into space. More water vapour = more clouds. From my understanding clouds have a net-cooling effect on the Earth to the tune of 20W/sq.m (Dessler 2010).
“Read the link and you will understand why”.
Thanks BBD. But I have no idea what specifically about my paragraph you thought was ‘nonsense’. I really haven’t investigated the Venus subject very thoroughly so the cause of the high-temperature on Venus is a mystery to me, adiabatic compression just seemed a probable cause. I will take a look at that later when I have time.
“So positive feedbacks are required for orbitally-triggered deglaciation”.
No, we don’t really know any of this. You are merely choosing to think that we do. It is all just conjecture. And because it is all supposed to have happened so long ago, we have no way of checking by direct observation whether any of it is true. This condition is absolute I’m afraid. There is no way around it and we only fool ourselves if we think that there is.
@Pekka
They changed the bond albedo, which is why every post you see on the web per-2012 (or 2011) assumes that the effective temperature of Venus is 230K as opposed to 184K.
That should read: pre-2012 (or 2011)
Trolling until he’s banned. I’d have done it a lot sooner than this.
There’s much more WV in the atmosphere than cloud. Hence (absorption spectra aside) the efficacy of WV as a GHG. You’ve also made a strong, false claim that clouds are “strong negative feedback”. As I said, it’s all wrong.
Of course we do. You are being obtuse. Almost no change in global total insolation and yet glacial termination. How might that work without a cascade of strongly positive feedbacks.
Think more, say less.
Peddlers of nonsense. Low climate sensitivity is incompatible with known paleoclimate variability – variability which could not occur if feedbacks net neutral or negative rendering the climate system insensitive to radiative perturbation.
You sound as if you think you know what you are on about, but frankly, you don’t understand much about physical climatology. Which is why you should avoid the peddlers of misinformation.
They have already made a monkey of you.
Will you please provide a proper reference for this claim.
This is not acceptable:
What you said was unequivocally a conspiracy theory:
Please don’t treat me – or others here – as if we are stupid.
Missed this bit of pseudosceptic agnosia:
See Berger (1978) Long-term variations of caloric insolation resulting from the Earth’s orbital elements.
Chipster,
I looked at the literature. It turns out that the estimates of the Bond albedo have varied over a wide range over the last 100 years at least. An estimate of 0.77±0.07 by Irvine (1968) was accepted by many, but values close to 0.9 have also been presented in several studies. It seems obvious that the analysis of Mallame et al led to the acceptance of the higher value of 0.90 for the Bond albedo of Venus. (That value applies to visible light, including UV and near IR of solar radiation lowers the estimate a little as the Bond albedos for the four bands studied by Mallame et al are 0.81, 0.90, 0.89, and 0.87).
Raymond Pierrehumbert gives the value 0.75 in his 2010 book on Planetary Climate. Thus you seem to be right in noting that the value of about 0.75 was the most commonly used.
I cannot, however, see much justification for your claim that the value of the albedo would have a fundamental influence on the understanding of the Venusian GHE. Even less changes in the comparison of Venus and Earth. These planets were and are very different independently of the changes and uncertainties in the understanding of Venus atmosphere.
Maintaining the convection consumes a significant amount of free energy.
Are you claiming this for any atmosphere, Pekka, or just an atmosphere with a strong greenhouse gas component?
For an atmosphere without GHGs, what mechanism besides thermal conduction could reduce lapse rate once established?
Gases have a low thermal conductivity. When conduction is the only mechanism for reducing lapse rate, a light breeze would suffice for convection to maintain lapse rate by overcoming conduction.
I admit I hadn’t considered radiation as a mechanism for reducing lapse rate on Venus. (It almost sounds contradictory given that you’re appealing to Venus’s GHE to infer maintenance of the lapse rate, but I think the two uses of radiation here can be separated, can clarify as needed.)
In solid state physics phonons and photons compete to increase conductivity, but I can see that in a near-liquid gas like Venus’s atmosphere the photons could well contribute much more to thermal conductivity than the phonons. Doing the math should show whether Venus’s 200 mph winds would be enough convection to overcome the photonic thermal conductivity. FWIW my intuition is that they would. I could believe that a sufficiently gentle breeze might not do it.
@me: Venus’s 200 mph winds
Oops, that’s only in the jet stream, sorry. Surface winds are more like Earth’s. According to Basilevsky et al, 2003, p.1707, “Closer to the surface, the wind velocity decreases, reaching less than a few metres per second at the level of the highest mountains of the planet. Near-surface winds are one of the major factors in exogenic resurfacing on Venus.”
Possibly the lower half of the atmosphere does require more than mere convection to maintain lapse rate, as you say. Remains to be checked.
Thank you Pekka. That’s interesting.
@c07: every post you see on the web per-2012 (or 2011) assumes that the effective temperature of Venus is 230K as opposed to 184K.
@BBD: Will you please provide a proper reference for this claim.
Second last table of http://bartonpaullevenson.com/Albedos.html : 230
Section 5 of http://www.atmos.washington.edu/2002Q4/211/notes_greenhouse.html : 220
http://www.atmos.washington.edu/2006Q1/211/assignment2_solutions.html: 220 (see “Unfortunately”)
http://lasp.colorado.edu/~bagenal/3720/CLASS14/14EVM-5.html : 264 (!)
http://ijolite.geology.uiuc.edu/05SprgClass/geo116/8-1.pdf : 227
http://www.gps.caltech.edu/classes/ese148a/lecture2.pdf: used 0.7 for albedo but didn’t do the math that would have given 220.
http://www.sonoma.edu/users/f/freidel/physical/204Ex3Malamud-Roam.htm : like the previous but with 0.8 instead of 0.7.
These were not cherry picked, they’re simply the first seven results of googling for
effective temperature of venus
(without quotes) that mentioned Venus. (Only the Wikipedia article on T_e didn’t.)
(Phew, glad I used 0.9 in my post on that question. 🙂 )
Vaughan,
The amount of free energy consumed depends on the amount of dissipation as dissipation works to slow down the convective circulation and all work converted in dissipative processes to heat must be provided by free energy in a way that makes the atmosphere capable of doing work. Thus a very quiet atmosphere with very little turbulence may retain convective circulation with little consumption of free energy, but a strongly turbulent one cannot.
The main atmospheric heat engine that drives the circulation is formed by heating a part of the atmosphere that’s warmer and located lower than those parts of the atmosphere that radiate the energy to space. The temperature difference must exceed the one based on adiabatic lapse rate before convection is initiated. (In other words the heating must raise the potential temperature at lower altitude above the potential temperature higher up.)
On the Earth the situation is clear. The main place where heating takes place is tropical surface and the most important cooling related to the heat engine occurs at extratropical upper troposphere. That pair drives Hadley Cells and Hadley Cells drive most of the other circulation.
On Venus the problem is that so little solar radiation reaches the surface. Thus the related heat engine has a small power. That may still be an important factor in driving the circulation, but perhaps the principal hot side of the heat engine is located higher up in the Venusian atmosphere, but still well lower than the regions that emit to the space. I don’t know enough about the Venus to tell. What I wrote above tells only about the general principles, but is also consistent with the little I know about Venus.
Thanks again, Pekka…
🙂
What I was trying to get chipster07 to do was to acknowledge that there was nothing suspicious, stealthy, devious or underhand in NASA’s behaviour. You have – I very much hope – helped to convince him that he is being paranoid.
@BBD: Not this nonsense [link to Colose’s old blog] again. Goddard was wrong, chipster07. Read the link and you will understand why.
Although Chris is very reliable in general, in this case he neglected Venus’s haze and clouds at 30-75 km. As I wrote (way) above I would expect this to change things to the extent that replacing the CO2 in Venus’s atmosphere by an equivalent (suitably defined) quantity of nitrogen should still leave some lapse rate below the clouds to heat up Venus’s surface.
However for Goddard and Motl’s explanation to fully explain 740 K Venus’s 8.2 K/km with no help from the GHE on Venus, Venus’s lapse rate would have to be left unchanged altogether by the radiation from the surface to haze and clouds, which as I guessed in my earlier comment seems unlikely.
VP,
Unless the haze and clouds contribute some kind of radiative forcing, I can’t really see why they’re all that relevant.
@Pekka: a very quiet atmosphere with very little turbulence may retain convective circulation with little consumption of free energy, but a strongly turbulent one cannot.
Sorry, not following. Are you saying that strong turbulence requires much free energy, or that strong turbulence impairs convective circulation? The former goes without saying, the latter I don’t understand. Have I misunderstood you?
To be honest, I’m not all that keen to see a debate about Goddard’s view of the greenhouse effect. It is almost certainly nonsense, and I don’t see any good reason why my blog should be used to spread such nonsense. Plus my only encounter with Stephen Goddard lead to me calling him a mendacious tw*t. I immediately regretted doing so, but have seen nothing since to convince me it wasn’tentirely justified.
@ATTP:Unless the haze and clouds contribute some kind of radiative forcing, I can’t really see why they’re all that relevant.
In their absence, and with a nitrogen atmosphere, all radiation would be straight from surface to space and Chris would be exactly right—an observer in space with FIR vision would see the surface. However all of Venus’s OLR is (by definition) coming from above unit optical depth viewed from space, which given how FIR-opaque the clouds are would be the cloud tops. Our FIR-vision space cadet would see only cloud tops at 70+ km and therefore receive FIR only from them and above.
ATTP
Yes, and my apologies. I was hoping to avoid exactly that but blowback seems to be the curse of the internet.
😉
VP,
I think, though, for that to be the case, the haze and clouds would need to be providing a large radiative forcing. I should probably read Chris Colose’s post.
Vaughan,
What I tried to say is that explaining strong and turbulent circulation requires that a powerful driver can be pointed out, and that I don’t really know what that is on Venus. It’s easier to explain that, when the surface is heated efficiently by the sun. The greenhouse effect helps surely essentially in that, but further details are required for a real explanation.
It is almost certainly nonsense
Sorry about that. On the rare occasions that I find even a grain of truth in what skeptics claim I’ve been in the habit of pointing it out. However I suppose I should stop doing that sort of thing, or I’d be marvelling 2n times a day on the correctness of n stopped clocks.
ATTP: I think, though, for that to be the case, the haze and clouds would need to be providing a large radiative forcing.
So far you’ve only defined “radiative forcing” for a disequilibrium state, which I believe you confirmed. AFAIK Venus has been in equilibrium for millions of years. What’s your definition of the concept for an equilibrium state?
@Pekka: What I tried to say is that explaining strong and turbulent circulation requires that a powerful driver can be pointed out, and that I don’t really know what that is on Venus.
Ok, good. I’d been assuming all along that ultimately the Sun was the driver of all activity above Venus’s surface and had merely been pointing to turbulence as the immediate proximal cause of convection sufficient to overcome all ways of compromising the lapse rate. I suspect we differ only on which parts of the causal chain we’ve been pointing to.
(My own “Venus fact sheet” is the (2.2 kg) book “The planet Venus” by Mikhail Ya. Marov and David H. Grinspoon, which I’ve found tremendously useful, it’s publication date of 1998 notwithstanding. All 26 of the missions to Venus (counting flybys and crashes) were during 1961-1989, giving M&G a decade to collate all that information and the ensuing literature. I bought it for $6 from betterworldbooks in 2010, there are still copies to be had for around $20 today. I suspect libraries are discarding it on the ground that it’s “so 20th-century” without realizing there have been no missions to Venus since 1989.)
On the matter of Earth climate sensitivity and cloud feedbacks, I think there’s a demonstration from paleoclimate that negative cloud feedback does not dominate in a warming world: the PETM.
This hyperthermal happened in a much warmer world than the present which it then made a great deal warmer. We can wonder why negative cloud feedback didn’t simply prevent the PETM from occurring (along with other Cenozoic hyperthermals) or we can infer that it doesn’t happen.
I decided to search for papers on the dynamics of the Venus atmosphere, and found this paper G. Schubert, S. W. Bougher, C. C. Covey, A. D. Del Genio, A. S. Grossman, J. L. Hollingsworth, S. S. Limaye, and R. E. Young: Venus Atmosphere Dynamics: A Continuing Enigma (AGU, 2007). It’s not surprising that I don’t know much about it as we can read from the paper statements like the following:
One more quote from the paper of Schubert et al.
This quote tells that the authors of the paper have thoughts, not very different from those presented in this thread. (Some by me, some by others.)
@TC: Holding the Earth sunless long enough to drop the GMST by 5 C (or doubling sunshine to raise it) would be more disruptive, but not more so than injecting 8680 ppmv of CO2 in the atmosphere on the same time scale.
1) The heat capacity of the oceans and specific latent heat of fusion of water at the poles (water is hard to freeze) might entail a longer wait for sustained night to reduce GMST by 5 °C than the various back-of-the-envelope calculations in this thread might indicate.
2) Life in hydrothermal vents would go on, but photosynthesizing plants would starve for lack of photons to convert CO2 to carbohydrates.
3) (Corollary of 2) The same day the Sun turned off, CO2 would start rising at 5 ppmv per month based on 123 GtC/yr of CO2 photosynthesized by plants.
If half of plant life had starved to death on account of 2) by the time the Sun turned back on, say in M months, then assuming the other half sprang enthusiastically back to life, the increase in CO2 level on account of 3) would continue at half that rate, 2.5 ppmv/month, or more if “sprang” and “enthusiastic” were not the operative terms.
Assuming M = 2 months and allowing 10 years for full recovery of plant life via a linear ramp-up (plant life being pretty hardy), the net CO2 increase at the end of 10 years would be 5*2 + 2.5*12*10/2 = 160 ppmv more than the expected increase with normal sunlight.
Assuming people get cracking on sustained night right away, Hofmann et al’s raised-exponential formula for atmospheric CO2 forecasts a 32 ppmv rise during 2015-2025, making the total expectation 160 + 32 = 192 ppmv over 10 years following 2 months of night, bringing us up to 592 ppmv, or 32 ppmv over twice the industrial level of 280 ppmv. More if after 2 months of night the GMST still hasn’t dropped 5 °C, which would then entail more dead plants.
With more time I’d break this logic into more digestible chunks, sorry about that.
Pekka, I see from that Schubert et al 2007 paper that I neglected to include ESA’s Venus Express, launched 2005, in my set of Venus missions, plus a couple of flybys on their way to Mercury and Saturn.
The oldest Schubert paper cited in Marov and Grinspoon is from 1969 on an experiment relevant to the Venus atmosphere. At the conclusion of Chapter 7 (pp. 330-331) on “Thermal regime and atmospheric dynamics” M&G cite Schubert et al’s 1980 paper “Structure and circulation of the Venus atmospere” as one of a couple of models of the zonal flow, which however this 2007 paper doesn’t cite (why?).
The possibility of stacked Hadley cells S et al 2007 refer to on p.101 is a phenomenon that I conjectured just 4 days ago may exist on Earth as a mechanism for the “missing” tropical hot spot.
(Hmm, I’d better not get too sidetracked by all this.)
Vaughn Pratt:
1) My calculation was off a bit. Based on the value for the heat capacity of the Earth given at this site, 10 sunless days would drop the Earth’s surface temperature by 1 C, and hence 50 days to drop it by 5 C.
2 and later) Plant deaths can be avoided by the simple expedient of extending the cooling period by two and allowing sunlight through for one day in two.
3) Are you seriously arguing that no mental model in physics should be admitted unless we have the technical capacity to implement it, at least in theory? Or that instantaneously increasing or decreasing CO2 content by a factor of 32 (the CO2 variation equivalent) could be done in less time and with less disruption? If not, this is a distraction from the point I raised above, not a discussion of it.
Just found where you defined radiative forcing:
ATTP: But a radiative forcing is – by definition – out of equilibrium.
By that definition, unless Venus is out of equilibrium it has no radiative forcing.
Thanks for explaining how you derived emissivity, namely as (255/288)^4 = 0.61. I’d been deriving it from the requirement that the derivative 4εσT^3 be 3.7 W/m2, making ε = 3.7/(4σT^3) which is 1 when T = 255 and 0.683 when T = 288. That was the only way I could think of making the derivative equal to 3.7 W/m2 at T = 288. It’s clearly a different notion from yours, namely the emissivity of the surface viewed from immediately above as opposed to that of the atmosphere viewed from space.
Since you agreed with Pekka that 0.61 didn’t make much sense by way of explanation of 3.7 W/m2 at 288K, and I don’t think my notion of emissivity is any better (because the only evidence for 0.683 is the number 3.7, which would be circular reasoning when deriving 3.7), I no longer see any satisfactory derivation of this number 3.7 W/m2. I continue to be unable to make sense of “keeping everything else the same”. Pekka’s comment earlier that “Vaughan seems to be right in criticizing the assumption of everything else staying the same as that assumption is not applicable to the problem discussed in the original post and in most comments of this thread.” reassures me that I’m not completely insane here.
I would summarize all this in the form of a criticism of Wikipedia’s article on climate sensitivity where it says (quoting Rahmstorf), “Without any feedbacks, a doubling of CO2 (which amounts to a forcing of 3.7 W/m2) would result in 1 °C global warming, which is easy to calculate and is undisputed.”
The criticism would be (i) that ease of computation is no evidence of sound logic, and (ii) that if not disputed then it should be. (This is a stronger criticism than what I wrote on that article’s talk page 14 December 2013 where I grumbled, in not so few words, that the assumptions needed to be stated (I suggested some) and that furthermore they were unlikely to be physical assumptions.)
If there’s a paper that already makes this point then it would nice to be able to replace the Rahmstorf quote with whatever it says. Otherwise someone is going to have to write one and get it published up to Wikipedia source standards.
@TC: Based on the value for the heat capacity of the Earth given at this site, 10 sunless days would drop the Earth’s surface temperature by 1 C, and hence 50 days to drop it by 5 C.
Excellent, that’s pretty close to the M = 2 figure (60 days) I guessed at.
However that site’s value has overlooked the fact that some of the mixed layer is going to start out closer to freezing than 5 C above freezing. How can you knock 5 C off that without extracting far more energy getting it below freezing? We need an estimate of how much of the mixed layer is currently below that temperature, which I don’t see at that site.
Plant deaths can be avoided by the simple expedient of extending the cooling period by two and allowing sunlight through for one day in two.
Good point. That would put them on half rations of carbohydrate for 100 days. That would raise M to 3 months.
One could actually do that experiment in a greenhouse in advance, or perhaps one greenhouse for every ten degrees of latitude, so say 12 greenhouses, as a safety check. Just shutter it every second day and see how the plants do.
Are you seriously arguing that no mental model in physics should be admitted unless we have the technical capacity to implement it, at least in theory? Or that instantaneously increasing or decreasing CO2 content by a factor of 32 (the CO2 variation equivalent) could be done in less time and with less disruption?
If I were serious I wouldn’t be hanging around blogs, I’d be writing papers. 🙂
But seriously, where did I suggest the former? Are you somehow inferring it from the inferences I drew from your suggestion of sustained night? I don’t see how those inferences imply any doubt as to our ability to do it, in fact I even predicated them on the assumption that we could do it in a year. If you have an estimate of when we could do it by I’d be happy to incorporate that.and revise my figures.
I don’t recall making any comparison involving the latter, nor even having thought about it.
Gotta go write a paper now.
VP,
If you want to estimate the total radiative forcing associated with the Greenhouse effect, then you can simply use
In other words the surface is emitting 150 Wm-2 more than is being emitted from the top-of-the-atmosphere and that means that there must be a net radiative forcing of 150 Wm-2 that balancing that difference.
What I mean with respect to Venus is that if the clouds/haze do not produce a radiative forcing then the surface will cool to the non-greenhouse equilibrium temperature of the planet. One issue with the clouds/haze on Venus – I think – is that the produce a large albedo (reflect of lot of the incoming solar radiation). If this was their only effect and if you replaced all the CO2 in the atmosphere of Venus with nitrogen, then that would suggest that the equilibrium surface would be lower than it would be without the clouds and haze. If the clouds/haze were to produce a surface temperature higher than it would be without them, that implies a net positive radiative forcing.
I have to go swimming with the kids again, but we can continue this later if need be 🙂
VP,
I’ll add one more thing about radiative forcings. A radiative forcing is – by definition – out of equilibrium. However, even in equilibrium, one can still determine the different contributions. For example, on the Earth we have CO2, water vapour and other greenhouse gases producing positive radiative forcings (totalling about 150 Wm-2 as I suggested above) and the increased surface temperature producing a negative feedback that balances these radiative forcings. So, yes, in equilibrium there is no net radiative forcing, but that just means that all the different contributions are in balance.
What radiative forcing means precisely is not intuitively obvious, a rough idea may be intuitive, but a precise definition not. As far as I know the only precise definitions are those given for deviations from equilibrium, and one of related alternatives has been picked as the definition of IPCC.
Similarly we have a rough idea of what no-feedback sensitivity means, but as far as I know that concept has not been defined in general terms independently of model implementations. Defining it precisely is difficult, because the division between basic “no-feedback” responses and feedbacks is artificial. It may have a clear meaning in a specific model implementation, but not in the reality.
Ambiguities of definition are often small enough to be of little concern. That’s most likely, when small deviations are being considered, and all responses are essentially linear and instantaneous. When nonlinearities and delayed dynamic responses are important people start to fill the gaps in definitions in different ways, and start to misunderstand each other. An argument that seems intuitively obvious for one is wrong for another. My feeling is that this thread is a good example of such problems. Reaching agreement is not possible as long as people do not use the same language, or perhaps even more fundamentally before people understand the mental models of each other as their use of language is built on those mental models.
From the TAR, Chapter 6, Radiative Forcing of Climate Change: IPCC (1990) and the SAR used a radiative forcing of 4.37 Wm−2 for a doubling of CO2 calculated with a simplified expression. Since then several studies, including some using GCMs (Mitchell and Johns, 1997; Ramaswamy and Chen, 1997b; Hansen et al., 1998), have calculated a lower radiative forcing due to CO2 (Pinnock et al., 1995; Roehl et al., 1995; Myhre and Stordal, 1997; Myhre et al., 1998b; Jain et al., 2000). The newer estimates of radiative forcing due to a doubling of CO2 are between 3.5 and 4.1 Wm−2 with the relevant species and various overlaps between greenhouse gases included.The lower forcing in the cited newer studies is due to an accounting of the stratospheric temperature adjustment which was not properly taken into account in the simplified expression used in IPCC (1990) and the SAR (Myhre et al., 1998b)……
The new best estimate based on the published results for the radiative forcing due to a doubling of CO2 is 3.7 Wm−2, which is a reduction of 15% compared to the SAR…..”
From this I would say that Rahmstorf’s Wikipedia quote is just wrong. 3.7 Wm-2 is an estimate based on a range from 3.5 to 4.1 Wm-2.
What may have been described once as simple is less and less so with each generation of IPCC reports. In AR5 a new concept Effective Radiative Forcing (ERF) replaces in many places the earlier RF. How complex the determination of radiative forcing has become is illustrated by Figure 8.1 of AR5 and by several pages of text in Chapters 7 and 8 of the report.
While the science presented in the IPCC reports is progressing, reading and understanding properly what the reports really tell has become very difficult. That’s in part due to the cumulative nature of the reports, where new reports are expected to tell mainly what has changed since the previous report. What we would need are well written and rather detailed textbooks that describe the present understanding emphasizing clarity and readability. That would make the outcome more openly dependent on the authors than the IPCC reports bound by formalized procedures, but not necessarily any less objective in practice.
==> “Reaching agreement is not possible as long as people do not use the same language, or perhaps even more fundamentally before people understand the mental models of each other as their use of language is built on those mental models.”
I think that there is a more basic step.
Reaching agreement is much easier when people are committed to reaching agreement. Instead, what we have in discussions about climate change are largely or even mostly affected by an overlap with psychological or cognitive “motivations,” in the sense of motivated reasoning. People are identified with one outcome or another, and so a “motivation” to be smarter or more correct or more insightful or more knowledgeable than others influences the discussion (psychological “motivations”). Or pattern-recognition biases influence people to re-shape new information so as to conform with existing conceptualizations rather than construct new conceptualizations based purely on the evidence at hand (cognitive “motivations”).
People who are committed to reaching an agreement are more likely to start with a discussion about how to work from shared definitions and models that integrate various individual perspectives.
As I got onto the bus after writing my second to last comment, I think I may not be quite correct. I’ve been trying to confirm my estimate because the last time I looked at this, I think I found that the overall positive radiative forcings associated with the greenhouse effect (mainly CO2 and water vapour) was more like 120 Wm-2, rather than 150 Wm-2, but I think my basic point still stands. You can’t have a surface that is warmer than the non-greenhouse equilibrium temperature without something that produces an effective radiative forcing. One way to consider this is what would the TOA radiative imbalance be if the surface had the non-greenhouse equilibrium temperature, but the atmosphere had the composition it has today. If it would be positive (i.e., we’d be gaining more energy than we’re losing) then that would be the effective radiative forcing, and the surface would need to warm to retain energy balance.
To follow on from what Joshua said :
I don’t know if I agree with this or not, but I do sometimes think people get fixated on terminology and don’t try to actually understand what others are trying to say. As long as people actually explain what they mean, there should be no reason why we can’t understand what we’re each saying, even if we aren’t all using precisely the same terminology. It is also just a blog, so I certainly regularly get it wrong and don’t really feel too bothered by that. There’s only so much time I can put into this and – at the moment at least – I’m quickly writing comments before throwing one of my kids in the swimming pool 🙂 .
I will add that I have found this discussion of radiative forcings quite confusing as I thought this was all pretty well established and not really something that should be producing a lengthy discussion. Nothing wrong with that specifically, but I’m still a little surprised.
Anders, you were correct the first time round. The total greenhouse effect is ~150 W/m^2.
Tom,
Thanks. I find I’m easily confused at the moment 🙂
Ah, the sorrow of it. Another fine mind gone to the drink.
🙂
@ATTP: the surface is emitting 150 Wm-2 more than is being emitted from the top-of-the-atmosphere and that means that there must be a net radiative forcing of 150 Wm-2 that balancing that difference.
So now you have two distinct notions, both of which you’re giving the same name, “radiative forcing”. One has value 3.7 W/m2, the other 150 W/m2.
Would it not be preferable to give them different names?
As long as people actually explain what they mean, there should be no reason why we can’t understand what we’re each saying, even if we aren’t all using precisely the same terminology.
Indeed. It would avoid superfluous precision in terminology if we called all animals dogs, and in the case of a lion explained each time that we meant a dog with a mane, and for an elephant a dog with a trunk. We would then understand what we’re each saying.
commenter with droll wit said: ” … if we called all animals dogs, and in the case of a lion explained each time that we meant a dog with a mane, and for an elephant a dog with a trunk. We would then understand what we’re each saying.”
That’s a very good suggestion – except horses also have manes. And “dog with a trunk” might be ambiguous as well. So as much as I admire the effort to make the language more efficient, at this point I think the proposal needs more work.
Philosophers agree, Vaughan.
> Would it not be preferable to give them different names?
http://rabett.blogspot.ca/2011/07/theres-word-for-that.html
VP,
Okay, the 3.7Wm2 is the change in radiative forcing that – by itself – would change surface temperatures by 1 degree. The 150 Wm2 is the total positive radiative forcing associated with the greenhouse effect. They’re the same basic concept. As others have pointed out, there are some complications to the definition of a radiative forcing, but in a simple sense the radiative forcing of some effect (increased GHGs for example) is by how much the system would be out of energy balance were that effect to occur.
Vaughn Pratt:
From the IPCC:
(My emphasis)
The bolded sections are the most germaine, and constitute a definitions of “radiative forcing” as properly used (without qualifying adjectives) in climate science. Given that definition, it is senseless to say that radiative forcing simpliciter has a value. You must always specify a change, either in conditions (CO2 concentrations etc) or in time. So, the radiative forcing of doubling CO2 concentration is 3.7 W/m^2 +/-10%. The long wave radiative forcing of removing all well mixed greenhouse gasses, water vapour and clouds from the atmosphere is –150 plus W/m^2 (with the plus being difficult to calculate and not relevant.) The total radiative forcing would be greater than that because of an increase in SW radiative forcing from clouds.
Being precise, for the removal of water vapour and clouds to be a forcing, we would need to remove all standing water (including oceans) from the Earth’s surface so that they did not replenish atmospheric water vapour in response to surface temperature. Absent that assumption, it is more correct to call the difference between upward LW flux at the surface and TOA the “total greenhouse effect”. But it is possible to set up a conceptual scenario in which the removal is a forcing, and hence in which we can talk about the compensating action in the atmosphere a radiative forcing.
None of this is conceptually difficult, nor particularly confusing. It is true that often people are a bit sloppy and talk about a “radiative forcing” when they should be talking about flux simpliciter. In such cases, however, it is not difficult to follow their meaning and it is also not difficult to set up a scenario in which their usage would be correct. Nothing hangs of this except (perhaps) a tendency to time wasting pedentry.
@ATTP: One issue with the clouds/haze on Venus – I think – is that the produce a large albedo (reflect of lot of the incoming solar radiation). If this was their only effect and if you replaced all the CO2 in the atmosphere of Venus with nitrogen, then that would suggest that the equilibrium surface would be lower than it would be without the clouds and haze. If the clouds/haze were to produce a surface temperature higher than it would be without them, that implies a net positive radiative forcing.
Since this is nominally a physics blog, and gedankenexperimenten originated in physics (or at least the name did), here’s a somewhat wacky gedankenexperiment that might bear on what needs to be taken into account in reasoning about Venus’s clouds after replacing the CO2 by N2.
While this experiment could be done on any planet, let’s start with Earth and move to Venus if and when the opportunity arises. For simplicity assume an axial tilt of 0 rather than 23° (so no seasons).
Extend the North and South poles (lower case pole, sufficiently strong) to height h. Attach to their tops a spherical mesh of radius R+h where R is the radius of the (spherical) Earth. The center of the sphere formed by the mesh therefore coincides with the center of the Earth, and the whole sphere floats at height h above the surface of the Earth. The mesh is really fine, passing 99.9% of all radiation incident on it.
Now wrap half the mesh with a hemisphere of very shiny foil, with an albedo of 1 on the inside and 0 (painted jet black) on the outside, positioned so as to touch both poles (i.e. the rim of the foil lies over a meridian).
Swing the mesh around Earth’s axis to point the foil away from the Sun and arrange to keep it that way (so that the Earth rotates under the mesh at exactly 1/1440 rpm, 1 revolution per 24.000 hours). This ensures that the foil is always in Earth’s shadow and so never blocks any sunlight. The result will be that the foil is absent from the sky at (solar) noon and covers the sky at midnight. At dusk the foil rises in the East and by 9 pm has covered the eastern half of the sky. At 3 am it covers the western half and sets in the West at 6 am.
Assume an atmosphere with a lapse rate of 10 °C/km and the usual oxygen and nitrogen but no greenhouse gases. Take the surface to be a black body (hence albedo 0, emissivity 1, Lambertian radiator), which without the foil would entail a surface temperature of (1367/σ)^{1/4} = 278.6 K, assumed the same everywhere (thanks to an infinitely thermally conductive lithosphere, say). Assume the foil also has the same temperature everywhere. Allow this setup to come to thermal equilibrium.
Question.
With h = 10 km, what are the temperatures of the surface and the foil?
The necessary reasoning might be more interesting than the actual number. Nevertheless it would be interesting if two people got the same numbers (and even surprising since more assumptions might well be needed to make the answer unique).
We can calculate the difference between LWIR emission from the surface and OLR and obtain the value of 150 W/m^2. It’s clear that this value is one quantitative measure of the strength of GHE.
We can also pick a linearized model and combine the temperature difference between the surface and effective radiative temperature of the Earth (33K) with the estimate 3.7 W/Km^2 multiplying them to get 122 W/m^2. This tells also about the strength of GHE in the same units.
We may dig deeper in the definition of RF and find out that it leaves open questions. In particular removing all GHGs but leaving clouds leaves part of the GHE. Thus the answer is more clear for ERF than RF in IPCC AR5 terminology. But then ERF tells that land temperatures are allowed to react opening a new problem.
The point of VP as far as see it (and a point I have tried to make as well) is that the issues are clear on qualitative level, but not quantitatively. Giving a numerical value tells little, if we don’t know precisely what’s the physical concept that this value is connected with. If we can link the value 150 W/m^2 to the right concept only because we know already, which of the plausible variables has that value, we have obviously not learned anything.
Being precise and explicit has value. Noting that may be nitpicking, but very often it’s more than that.
Yes, I do think that much of the confusion about the manuscript discussed in the original post and much of the rather useless argumentation of many comments of this thread are caused solely by the lack of precise and explicit definition of what’s being discussed.
Perhaps the whole blogosphere would be much more quiet (and boring?) without the mutual misunderstandings caused by interpreting the same words and expressions differently.
@me: The result will be that the foil is absent from the sky at (solar) noon and covers the sky at midnight. At dusk the foil rises in the East and by 9 pm has covered the eastern half of the sky. At 3 am it covers the western half and sets in the West at 6 am.
Oops, that’s wrong. For h = 10 km, at dusk the leading edge of the foil flies overhead east to west at supersonic speed to hide the stars before they’re properly visible in the twilight, and at dawn the trailing edge does the same to reveal the dawn sky, the stars having faded. Nighttime astronomers miss out completely.
@PP: Perhaps the whole blogosphere would be much more quiet (and boring?) without the mutual misunderstandings caused by interpreting the same words and expressions differently.
Never attribute to misinterpretation that which is adequately explained by ideology.
But otherwise I agree with you right down the line.
Pekka,
That’s what confused me about my initial calculation. Without wanting to start a lengthy discussion, I think the difference is whether you want to define the RF with respect to the TOA today (i.e., with the greenhouse effect operating) or relative to the non-greenhouse TOA (the surface).
VP,
If I understand you scenario, the foil is always on the night-side and blocks all outgoing radiation. Then I think one could solve this using
i.e., the amount of energy the planet receives is determined by its cross-sectional area and the flux from the star (left-hand side). Given that the foil blocks all outgoing radiation on the night-side, all of the energy emitted by the planet comes only from the day-side hemisphere (right-hand side).
Of course, I should probably wait until I get back from my holiday before responding to this as I’ve probably missed something. As Pekka says, though, the blogosphere would be boring if we didn’t just jump in and have a go.
Pekka,
If it is the case that the issues are clear qualitatively but not quantitatively, then some are not doing a particularly good job of making this clear.
I don’t actually understand what you’re getting at here. Given that every time I’ve expressed a quantity I’ve also shown the equation I’ve used to determine that quantity, I would have thought that the connection was evident. I also don’t follow your last sentence. If I know certain quantities and can use them to determine some other quantity, I’ve learned something. That’s a fundamental part of doing science, isn’t it?
I have a somewhat different interpretation to this discussion than that of Pekka. To me, this appears to be a situation where some who don’t properly understand the concept of a radiative forcing are complaining that those trying to explain it are not being sufficiently precise and aren’t always using the correct terminology. They may have a point, but if you try many different ways to explain something and try to make it simple enough to understand, it’s quite likely you’ll end up talking yourself in circles.
@VP: Never attribute to misinterpretation that which is adequately explained by ideology.
I’ll always do that occasionally, as the alternative is to err too often in the opposite direction.
@ATTP: To me, this appears to be a situation where some who don’t properly understand the concept of a radiative forcing are complaining that those trying to explain it are not being sufficiently precise and aren’t always using the correct terminology.
Often there are two (or more) alternative interpretations:
– They have not properly understood the concept.
– They have understood, but do not accept the way it’s being used and try to argue for a change in that.
Coming back to the first point. My preference is to allow for a benefit of doubt in favor of those asking questions, including stupid questions as long as the evidence against their good will and honesty is not overwhelming.
Some of the others commenting to this site seem to consider it essential that such people are driven out immediately (allowing for zero benefit of doubt). In my view these commenters have far too little trust in the audience of this site. They are afraid that seeing stupid claims on this site is damaging even when none of us can affect their prevalence on sites with a much more receptive audience. They do not accept that the most stupid claims are inconsequential (can be left without any reaction), and that the best way of reacting to the less stupid but still wrong ones is to take advantage of them as a basis for explaining the issues correctly. When it’s not possible to explain the issue correctly, the likely conclusion is that the claim was not stupid at all (it may still be wrong, but concluding even that might require reservations).
As far as I have understood, the original idea you had in starting to blog is exactly what I support in the above. It’s, however, difficult to communicate effectively with people of different background. It’s worthwhile to be careful in the formulation and to try to remember that they fill all the gaps of the text differently, possibly very differently, from what you consider obvious.
===
Repetitive claims on points that have already been discussed many times are a different issue, there’s no need to allow spamming of that type, but again some care should be taken in concluding that the point has really been answered as well as it should have been answered.
Vaughn Pratt, interesting thought experiment.
At 10 km, the foil is well within the troposphere. The foil is infinitely conductive, has (I presume) very low thermal mass, and is perfectly reflective on the side facing the Earth. Ignoring radiation, it will receive energy and pass it on through collisions with the atmosphere both above and below it. It will prevent the direct passage of air by convection, but convective cells will pass on more energy, which will, however be equalized over the hemisphere. Ignoring radiation, therefore, its temperature will the hemispheric average for the atmosphere at 10 km, as determined by the lapse rate, plus any additional warming from friction (which I assume is intended to be zero).
The foil, however, receives no radiative energy from below, but receives radiative and emits radiative energy from above. The radiative energy from above (the optically thin and cool upper atmosphere) will be significantly less than the energy received from the lower atmosphere by collision, and can be ignored. Therefore the effect of the radiation will be to cool the foil significantly, thereby also cooling the atmosphere above and below it further.
The net effect, ignoring the disruption of hadley cells etc, would be to greatly enhance the greenhouse effect. Some additional sunlight would be captured due to the edge of the foil capturing additional sunlight, but at h = 10 km, the additional sunlight captured is small. The diurnal temperature range would also be reduced both due to that additional sunlight (which would fall in the night hemisphere) and due to reflection of emissions and reflected light from daylight zones to night time zones near the edge of the foil. Overall, however, the Earth would be much cooler than now.
If we assume that the foil is perfectly insulated against energy from the atmosphere, Ander’s solution above captures the essential maths.
Pekka,
My preference would be for all to give the benefit of doubt. I wasn’t implying nefarious intent, simply that some seem to have a higher expectation of others than of themselves.
Tom,
hmm, I knew I should have thought about it a little more.
Ander’s, I was going to draw your attention to this xkcd cartoon:
http://xkcd.com/1158/
Vaughn’s thought experiment gives me the best excuse I will even have.
Off topic – I’ll understand if this gets deleted:
Tom Curtis –
I ran across this statement from McIintyre, and was hoping if you could confirm its veracity:
==> “Both Cook and Lewandowsky were, of course, involved in a previous incident also involving lying, a conclusion which Tom Curtis of SKS also reached: see here here.”
The amount of energy that goes into these food fights is always amusing to me, and all the Jell-o flinging certainly obscures anything important related to the science of climate change – but I was curious to know whether that comment from McIntyre is accurate. ( I certainly don’t take the time to follow all the comments in all the related threads) Did you reach a conclusion that both Cook and Lewandowsky lied?
(of course, parsing McIntyre’s grammar closely, what he actually says is that you agree that they were involved in a previous incident involving lying – which could actually mean that they were involved in an incident where someone else, say McIntyre, lied. But I kind of doubt that was his intended meaning. 🙂 )
@TC: ignoring the disruption of hadley cells etc,
Excellent point, Tom. Blocking the vertical component of the cells at night would have them waiting like cars camped out overnight at a railway crossing while a very long train passed. (If overnight sounds bad pity the poor trucks crossing the Zambezi River at the Botswana-Zambia border that have to line up for two weeks waiting their turn for the Kazungula ferry. My wife and I crossed there last month but via van then motorboat then different van, so no waiting.)
One possibility would be to put seven slots in at the integer multiples of 30° to permit the vertical components to pass through during the night (the foil is not obstructing during the day).
However this raises the very interesting question of whether Hadley cells run steadily. Possibly not, on the ground that all six are driven like gear wheels primarily by thermals near the equator that start up late morning after the Sun has had a chance to warm the ground and destabilize the lower troposphere (the main driver of lapse rate), and die back down in the evening as the lower troposphere cools and regains its stability. If that’s correct then there should be relatively little disruption other than of the residual momentum of the vertical components during the evening. The horizontal components should be much longer than needed to act as an atmospheric hammer absorber.
No answer from to my question to Tom Curtis here – but i see that he did leave a comment over at Stevie Mac’s blog.
To which McIntyre left this lame response:
I followed up with a comment of my own – which went into moderation. We’ll see if it clears:
Your comment is awaiting moderation.
Tom Curtis –
==> “I expect a retraction of your claim, and an apology for misrepresenting me again on a point on which you have already had to correct yourself.”
Good luck expecting that apology. It struck me as likely being inaccurate when I first read it (over at ATTP I asked you for verification). So it is interesting to find out from your comment that Steve wrote that even though he was quite familiar with what you’ve said and could easily have fact checked it in any case.
But now I read that he has misrepresented you in this way before, and already had to correct himself on the issue? So the question might be asked whether the error was inadvertent or sloppiness (as I originally assumed), as opposed to deliberate.
But even after all of that, you’d think that he’d respect your request for an apology. Instead, he offers that you misinterpreted him?
Too funny.
Methinks that auditors should audit themselves.
Joshua, I have replied to Steve at Climate Audit, and he has partially corrected the offending sentence. To be clear, I believe Cook to have been honest and to have no evidence to the contrary. I cannot now remember the details of the case sufficiently to remember whether or not it showed dishonesty by Lewandowsky, so that even as amended the statement does not reflect my current views. I have no desire, however, to be drawn into the morass of that issue again. Involvement in that issue has proven to me that “skeptics” in general have no desire for reasonable dialogue, and are only interested in garnering “gotcha” statements.
I saw that, Tom. Thanks. I posted a response here that is in moderation.
I respect your reasons for not wanting to get dragged into it again, but I think that McIntyre’s misrepresentation of you (and failure to comply with your request for an apology) merits some attention. I posted a comment at his blog, but it landed in moderation. I also reposted it here but it landed in moderation here also! 🙂
I’ll wait to see if my comment gets liberated here, or there. I will also post on it at Judith’s since she linked to Steve’s post on her blog.
I’ve released your comment, Joshua. Quite a few comments are ending up in moderation at the moment for no apparent reason. I don’t get notification of their presence there either so if there’s a delay before their approval then it’s because I don’t know they’re there. I try to check fairly regularly though.
Vaughn Pratt, the foil would disrupt descending air currents as well. Further, the very great radiative cooling at precisely 10 km would generate sufficient of a lapse rate above and below the foil to maintain convection immediately below the foil during the night and downdrafts above it, but with no connection between the two, and leave a cool region at that altitude at sun up, forestalling the large convective circulation from below during the day. Without running the experiment on a GCM, I do not know the result would change the Hadley circulation significantly, but the suggestion it would not is intuitively implausible. Nor would seven slots be enough to avoid disruption. Updraft and downdraft rates are relatively slow, and if not connected over a wide spread and diffuse area would not have the same effect.
@PP: Some of the others commenting to this site seem to consider it essential that such people are driven out immediately (allowing for zero benefit of doubt).
That behavior makes it very hard for newcomers to break into the discussion. In February 2011, not having previously heard of either Tamino or his blog, my attention was drawn to it by willard.
Frank O’Dwyer had commented, “Vaughan Pratt has a nice simple analysis which uses simple smoothing to remove the effect of the AMO. The result is striking.” to which Tamino had responded, “Sorry, but I don’t buy it. He hasn’t removed the impact of AMO, he’s just removed the fluctuations on a 65-year timescale.” .
Unaware that I’d done more than remove the fluctuations, I signed up for the blog in the hope of finding out what he thought I’d done wrong, linking to my (very primitive) work to date in case it helped. Unfortunately none of it carried any weight with Tamino, who accused me of not understanding the statistics of period analysis (given what he wrote I might say the same of him) and of denying the physics of aerosol cooling (which he based on my impression that people were estimating the extent of that cooling from temperature data—Tamino insisted that it could be quantitatively estimated from the impact of volcanic eruptions). He concluded with “I think your theories have no merit. I respect your civility. But no, I don’t wish to argue with you about it.”
While I was unable to reciprocate his respect, it was clear that saying so would be counterproductive. Having no idea what he meant by “your theories”, I responded at greater length in the hope of clarifying things, all of which he deleted saying “this is not your blog”.
Tamino claimed he’d proved statistically that the phenomenon others were calling an oscillation was not an oscillation. Instead it was “due to an early-20th-century lull in volcanism, early-20th-century increase in solar activity, and huge mid-century increases in anthropogenic sulfate aerosols.” While intuitively it seemed unlikely to me that those influences could be that strong, I had no concrete numbers to back up my intuition and so continued to remain as neutral on the matter as I had been prior to 2011. Having no idea what I could have said differently to avoid his wrath, short of “you’re right and I’m wrong”, I let the matter drop.
Then last year it occurred to me that there might be enough information in the separate CRUTEM4 land and HadSST3 sea global mean temperatures to confirm or refute Tamino’s opinion. I was very surprised by just how much information there was. Slide 4 of my AGU Fall Meeting talk shows that whenever the (3-7-weighted) land-sea sum (essentially HadCRUT4) rose, the (unweighted) land-sea difference either declined strongly (1860-1880), weakly (1900-1945), or rose strongly (1970-2000). Slides 5-9 give an elementary account of the physics underlying the conclusion that the first warming was mostly generated somewhere below the surface, the last one mostly from above (presumably mostly CO2 forcing), and the middle one somewhere in between (consistent with the onset of CO2 forcing). (NOAA’s estimate of some 2000 W/m2 of heat exchange between the ocean and the atmosphere during tropical storms answers the question of the geophysical counterpart of the copper rod.)
Tamino can at last truthfully say that I deny that aerosol cooling contributes in an essential way to the evident 2.5 cycles of oscillation in HadCRUT4.
Slide 28 superimposes the (suitably smoothed and scaled) ESRL AMO index and the residual from smoothed HadCRUT4 after removing the expected contribution of rising CO2. Tamino claimed to have a statistical proof that the former was not an oscillation, without however stating either the criterion to be one or the confidence level in this case. If the criterion is at all reasonable for this situation, and the confidence level is at least 95%, I’d be fascinated to see the proof. However if the criterion starts out with the arbitrary requirement of at least three full cycles then of course game over as far as either HadCRUT4 or the ESRL AMO index is concerned, since there are only 2.5 cycles. One would then need to fall back on longer datasets such as CET, or the recently released BEST sea surface data, to meet such a stringent criterion.
Part of the problem I suspect is that Tamino’s experience is with period analysis of variable stars where of course 3 cycles is an insignificant blip. But what might work to refute periodicity for a variable star might well also refute periodicity within a wave packet, and there I suspect he’d find himself on weaker ground.
Tom,
Good points re Hadley cells. I agree it would take a GCM to settle this.
the very great radiative cooling at precisely 10 km would generate sufficient of a lapse rate above and below the foil to maintain convection immediately below the foil during the night and downdrafts above it
With a lapse rate of 10 K/km, if the surface temperature were 300K then the foil, in good contact with the atmosphere, would be at 200K, and hence could only radiate 90.7 W/m2 to space. Is that consistent with your picture?
Looks like you and Anders are the only ones offering analyses so I’ll comment on them shortly.
Vaughn, I have probably been under thinking the hadley cells in that making the entire surface superconductive so that the temperature is everywhere the same will probably destroy the Hadley cells anyway.
To make the scenario more tractable, I will assume negligible atmospheric absorption or scattering of visible and near infrared radiation, but that the greenhouse effect prior to installation of the mesh plus foil is equal to current levels. Given this, at time of installation, the surface temperature everywhere will be 288 K. That means the initial temperature of the foil will be approximately 188 K (approximately because there would be a net energy loss to molecules above the foil). Initial emissions from the TOA after installation would be 238 W/m^2 from the sunlit side, and 71 W/m^2 from the foil, resulting in an average global emissions of 155 W/m^2 after installation. The large forcing (84 W/m^2) would result in a very rapid warming of the Earth’s surface afterwards, until average emissions were again 238 W/m^2. The exact surface temperature resulting in that increase would depend on how high the effective altitude of radiation to space was raised by feedbacks on the day side, so I won’t pretend that I can calculate it even approximately.
Ok, so Anders original solution has Earth’s cross-section times the solar constant on the left hand side (total insolation) and half the Earth’s surface times σT^4 on the right (total OLR from the day half of the planet). This should give 1.189 (the fourth root of 2 or three equal-tempered semitones) times the value 278.6 K in the problem statement, or 331.3K.
Implicit in this solution is that the foil cools to 2.7K, in equilibrium with space, radiating 3 microwatts/m2. Tom, you included the lapse rate to keep the foil warmer, excellent, with which I take it Anders now agrees. But unlike Anders you did not suggest suitable equations, and I’m guessing that your “To make the scenario more tractable,” means you won’t be offering one for the no-GHG case.
However ignoring messy details like Hadley cells, and whether the foil changes the lapse rate, and assuming no GHGs as per the original problem, it’s not hard to see what the equations should be.
Let S and T be the respective temperatures of Earth’s surface and the foil, and let A be the cross section of Earth (whence 2A is the area of a terrestrial hemisphere). Then
1. T = S − 100 (lapse rate of 10 K/km at 10 km)
2. 1367A = 2Aσ(S^4 + T^4) (LHS = total insolation, RHS = total OLR)
2 simplifies to S^4 + T^4 = 1367/(2σ), call the RHS Q (= 1.2054E-10) and rewrite 2 as
2′. S = (Q − T^4)^{1/4}.
Setting S = 0 as a rough initial guess and iterating equations 1 then 2′ to convergence, that is,
T = S − 100
S = (Q − T^4)^{1/4}
yields after nine steps (I did this manually with bc in Cygwin — Linux has the same capability — by typing the assignments on one line and then hitting UP-ARROW ENTER nine times):
S = 315.43 K = 42.28 °C = 108.1 °F
T = 215.43 K = −57.72 °C = −71.9 °F
So Anders’ original solution would be 16 °C higher than Tom’s on account of neglecting atmosphere warming the foil.
Daytime OLR is therefore 561 W/m2 (from the surface) and at night 122 W/m2 (from the foil).
Please check all this in case I’ve screwed up somewhere.
Any opinions on what impact 122 W/m2 of foil cooling might have on the lapse rate between 9 and 10 km? Will it lower it or raise it? I guess it would depend on how forcefully the lapse rate is maintained in the absence of the foil. The above calculations assume no impact.
The point of the silver bottom on the foil was to avoid worrying about how radiant heating of the foil would interfere with the atmosphere’s control of the foil’s temperature. I would guess that painting the whole foil black would be a lot trickier to analyze because we don’t know how fast lapse rate can cool the foil to offset the radiative heating from the surface.
Which is similar to the problem we faced in the analysis of a nitrogen atmosphere for Venus without removing the haze and clouds.
Which was the point of my gedankenexperiment.
Knowing the albedo of the bottom of the haze at FIR would help.
Vaughn the equation for surface temperature, S, in the no atmospheric GHG case would be:
0.7*1361/4=σ*(S^4+(S-100)^4)/2
I will leave simplifying it to people with more experience in algebra than my limited exposure. The 1361 W/m^2 for TSI is in line with more recent estimates based on the SORCE satellite. By all means use 1367 W/m^2 if you prefer. Using a brute force search on a spread sheet, the surface temperature is approximately 290.2 K. The equation differs from your equation by treating (1-albedo) as a factor on the LHS rather than albedo as a factor on the RHS.
Technically that assumes the existence of cloud albedo on the daylight side (and hence contradicts the claim that there is no greenhouse effect on the daylight side. We can assume there is additional snow and ice on the ground or use a lower albedo. Using an albedo of 0.15 the surface temperature rises to 303.5 K.
Assuming a constant GHE on the daylight side (ie, the no feedback case), we can determine the effective altitude of radiation to space on the daylight side to be 3.3 Km, and give the formula as:
0.7*1361/4=σ*((S-33)^4+(S-100)^4)/2
In that case the equilibrium temperature surface temperature would be approx 314.5 K, a figure that is only the crudest ball park estimate because too many factors are altered to be confident feedbacks will behave as they currently do.
This is all very fun in the “imagining is fun” sense, but how does it related to the OP or recent discussion of radiative forcing?
Vaughan,
Okay, I didn’t read your gedanken experiment carefully enough. My solution was for the effective temperature only and I hadn’t appreciated that the foil would radiate. I’m not quite sure that I’m getting the point though. I think there is still a way to cast the effect of the foil as producing a radiative forcing.
You’re also assuming – I think – that the surface temperature is the same in both hemispheres, even though one is in sunlight and the other is dark. It’s not obvious to me that this assumption is justified.
Vaughan, in regards your AGU presentation – have you ever visited ContextEarth? You might like to look at the posts in this series.
Pingback: Holiday almost over | And Then There's Physics
I think there is still a way to cast the effect of the foil as producing a radiative forcing.
Ok, but you need to explain what you mean by “radiative forcing” in this case. In another context, with one meaning you’ve obtained 3.7 W/m2 and with another 150 W/m2. Two people can only agree on the value of something when they’ve agreed on what that something is.
You’re also assuming – I think – that the surface temperature is the same in both hemispheres, even though one is in sunlight and the other is dark. It’s not obvious to me that this assumption is justified.
Good point. Can we agree on a definition of “surface temperature” as “running mean over 24 hours”? Would that take care of your concern?
VP,
I thought we’d clarified this. The radiative forcing is not a single number. It is, essentially, how some change will influence our TOA energy balance. The 3.7 Wm-2 is simply the change in radiative forcing that would – by itself – change surface temperatures by 1 degree. The 150 Wm-2 is the total radiative forcing associated with the greenhouse effect (in which surface temperatures are 33 degrees higher than they would be in the absence of the greenhouse effect). As Pekka points out, one could argue that the radiative forcing associated with the greenhouse effect should be 122 Wm-2 (i.e., 3.7 Wm-2 multiplied by 33 degrees) but I think that the subtlety associated with these two values is not worth exploring here (unless you really want to).
If you consider your hypothetical scenario, you have one hemisphere that radiates from the surface of the planet, and one that radiates from the foil at an altitude of 10 km. The effect of this is to increase the average surface temperature. If one defines the surface temperature with the foil in place as
and the surface temperature in the absence of the foil as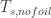 
, then the effective radiative influence of the foil could be regarded as
In other words, if the system were in equilibrium without the foil (in which case the emitting surface is the surface of the planet) and the foil were instantaneously put in place, at the instant in which the foil is in place the surface would have the above energy imbalance and would warm to return the system to energy balance.
We could do so and if we did then your solution would seem correct. The problem I would have with this definition is that the temperature at the altitude of the foil on the night-side will, presumably, be set by the surface temperature on the night side, which would (I think) typically be lower than the surface temperature on the day side. I, however, can’t immediately see how one would determine this difference and so I can’t see how to include this difference in your gedanken experiment.
@KO’N: Vaughan, in regards your AGU presentation – have you ever visited ContextEarth? You might like to look at the posts in this series.
Thanks very much for that pointer, Kevin, I hadn’t run into it before.
At a quick glance it seems to be focused on periodic and quasiperiodic phenomena with periods below 20 years. Is that a fair assessment or do they also consider longer periods somewhere?
This brings up the question of the definition of “climate”. The first FAQ at the WMO’s site asks “What is climate?” and says “The classical period is 30 years, as defined by the World Meteorological Organization (WMO).” But this is simply repeating what the IPCC says about the WMO, creating an interesting circularity in the alleged WMO’s definition. Anyone have a more direct source for this definition?
The IPCC itself defines TCR as “the change in the global mean surface temperature, averaged over a 20-year period, centred at the time of atmospheric carbon dioxide doubling, in a climate model simulation in which CO2 increases at 1%/yr.” Being a stickler for exposition I would have broken this sentence into two concepts, 20-year climate and TCR: “Defining climate as the centered 20-year running mean of the GMST, TCR is the change in climate over 70 years when atmospheric CO2 rises at 1%/yr.” (70 years or doubling CO2 is essentially the same thing at a CAGR of 1% so either is fine.)
20 years is preferable as a notion of “climate” because 30 years may be a bit too long for interpreting what’s been happening over the past half century. This is where the recent rise has been clearest, and if the CAGR of CO2 emissions continues to double every half century (it was 0.25% in 1960, has been 0.5% lately, and should easily hit 1% by 2060), the coming half century will see even faster change.
My preference therefore is to understand climate at any instance as the mean and the trend (two separate numbers) over the period from 10 years before to 10 years after, i.e. centered 20-year running mean-and-trend (two curves).
For this reason I’ve been ignoring solar cycles, ENSO, the Chandler wobble, and other “fast” phenomena as having no relevance to 20-year climate. If there’s evidence to the contrary I would certainly pay them more attention.
I was remiss in not being more explicit about this in my talk, which would have been better packaged as evidence for sticking to 20-year mean-and-trend climate in assessing the relevance of the physical basis to the latter half of the 21st century.
@ATTP: if the system were in equilibrium without the foil (in which case the emitting surface is the surface of the planet) and the foil were instantaneously put in place, at the instant in which the foil is in place the surface would have the above energy imbalance and would warm to return the system to energy balance.
Thanks, that answers my question (but the preceding thought processes going into it are helpful).
The problem statement gives the pre-foil temperature as 278.6K, corresponding to 1367/4 = 341.75 W/m2. Assuming the inserted foil equilibrates immediately with the atmosphere it will be at 178.6K and therefore radiating 57.7 W/m2. Total radiation averaged over the whole planet is therefore their mean, 199.7. The immediate disequilibrium forcing (IDF) is therefore 341.75 − 199.7 = 142 W/m2. (I made up the name IDF just now but will go with whatever name people think is preferable. This business of using the same name for radically different concepts wastes time in clarifications that could have been avoided in the first place with mutually agreed-on terminology.)
The problem I would have with [the 24-hour] definition is that the temperature at the altitude of the foil on the night-side will, presumably, be set by the surface temperature on the night side, which would (I think) typically be lower than the surface temperature on the day side.
No because the foil is shiny below. Someone on the ground looking up at the sky sees their mirror image above, standing on mirrored ground having the same temperature as the ground itself. Therefore no heat is lost. Another way to see this is that all heat radiated up is reflected straight back down. The shiny foil is in effect a Thermos flask keeping the night surface exactly as warm as it was 12 hours earlier, no warmer and no cooler, throughout the night. A perfect insulator.
The foil itself is very cold, but its lower side has emissivity 0 (Kirchhoff’s law of thermal radiation) and hence radiates exactly nothing to the surface. All the radiation received from above by the surface is its own upward radiation reflected back down by the shiny foil.
VP,
Then I’m slightly confused about your solution. If the foil radiates nothing to space, then doesn’t that mean that all of the energy lost to space must come from the day-side which then means that my original solution is correct, doesn’t it? Your solution was
where
was the temperature of the foil – set by the lapse rate – and 
was the temperature of the surface. This doesn’t seem quite the same as you’ve just described.
If the foil radiates nothing to space,
That would be the case for the unpainted foil. Painting it black on the outside allows it to radiate to space.
VP,
But if the foil radiates to space, the night-side must be losing energy and it will cool since it has no source of energy.
But if the foil radiates to space, the night-side must be losing energy and it will cool since it has no source of energy.
Good point, and I see I omitted an assumption I’d been making. The atmosphere is coupled thermally to the foil, via convection (to bring heat up from below) and conduction (to get it into the foil—shininess is only a barrier to radiation, not conduction). I was assuming that this convection and conduction had sufficient flow to balance the radiative loss to space, but neglected to say so.
The problem becomes much harder when the flow from the atmosphere to the foil is insufficient to offset radiative cooling to space. For one thing this increases the lapse rate immediately below the foil.
@me: For one thing this increases the lapse rate immediately below the foil.
…and therefore makes the atmosphere unstable there, thereby initiating and accelerating convection. I’d guess that with the very low radiation to space at that temperature that this instability would easily be able to replenish the heat lost to space by the foil—it should be a self-regulating process.
VP,
Sure, I’d kind of assumed that, but it still means that the night-side is losing energy and so should cool. Having said that, it would be fairly easy to see what impact this energy loss would have on the temperatures over the course of 12 hours. It might be, essentially, negligible.
VP,
Okay, if the foil radiates at 57.7 Wm-2, the night-side loses 6 x 1020 J over the course of 12 hours. The mass of the atmosphere is around 2.5 x 1018 kg and has a heat capacity of 1000 J kg-1 K-1, so it take 2.5 x 1021 J to change the temperature by 1 degree. So, it sounds like the energy loss over the course of one night won’t change the temperature of the atmosphere by very much so your initial assumption is probably pretty good.
@TC: The equation differs from your equation by treating (1-albedo) as a factor on the LHS rather than albedo as a factor on the RHS.
I would have said it differs by bringing in albedo. The only albedos in the problem are 0 and 1.
This is all very fun in the “imagining is fun” sense, but how does it related to the OP or recent discussion of radiative forcing?
It was in response to Anders’ question as to how clouds on Venus could be relevant in the absence of greenhouse gases. I designed my problem to give practice in thinking about that sort of thing, with the details chosen to make the problem solvable. There should be a number of such problems in between the Venus clouds problem and my problem, raising various issues with varying degrees of difficulty.
VP,
With regards to this comment of yours,
I don’t think the concepts are radically different. All of those quantities I’ve called “radiative forcings” are essentially the same concept, even if the quantities are different.
Okay, if the foil radiates at 57.7 Wm-2
That was the radiation when the foil was inserted, prior to the surface warming up due to no longer losing heat at night. I believe what you’re asking about should be the radiation from the foil after the surface has reached equilibrium, which is 122 W/m2.
The mass of the atmosphere is around
That assumes that the cooling foil cools the atmosphere uniformly. It might cool just the top 100 m. Pressure at 10 km is about 300 mb, so a 100 m high column of air of cross section 1 m2 at that altitude would have a mass of only 30 kg and hence a heat capacity at constant pressure of 30 kJ/K. If that 100m column received no warmth from below, 122 W sustained over 12 hours would drop the temperature 175 K.
Which it couldn’t sustain because the foil would radiate less at lower temperature, and furthermore the atmosphere would get extremely unstable. More likely is that the top 1 km would cool by 17 K. But even that sounds hard to sustain over 12 hours, so perhaps you’re right that the whole atmosphere has to chip in to keep the foil warm. Maybe there’s a linear gradient to the surface and the foil loses say 4 K. Interesting problem.
VP,
My calculation is simply determining how much energy is radiated by the foil out into space in a given time interval (12 hours). I was wrong by about a factor of 2, so that isn’t that important. Given that the foil gets its energy from the atmosphere below, the energy it radiates therefore determines how much energy is being lost by the atmosphere. However, it doesn’t appear particularly substantial (it may change the average temperature by a fraction of a degree) and so your assumption of an average surface temperature seems reasonable given this is really just meant to be illustrative.
I don’t think the concepts are radically different. All of those quantities I’ve called “radiative forcings” are essentially the same concept, even if the quantities are different.
What you’re calling radiative forcing in the case of equilibrium is actually the radiative forcing in the case of disequilibrium at the moment of adding the forcing agent. As the system drifts towards equilibrium there is a decreasing residual forcing that vanishes in the limit. In the limit you then redefine the forcing to be what it was at the beginning of that process instead of zero. I would call that a radical redefinition of “forcing”.
VP,
Maybe I haven’t always been as clear as I should have been, but when I’ve used the term radiative forcing it has always referred to how the forcing agent influences the energy balance prior to the system shifting back into equilibrium. However, even in equilibrium one can determine the influences of the different processes to determine what their radiative forcings would be.
Sure, and in equilibrium the net radiative forcing is zero, however that doesn’t change the radiative influences of the different forcing agents.
@ATTP: However, it doesn’t appear particularly substantial (it may change the average temperature by a fraction of a degree) and so your assumption of an average surface temperature seems reasonable given this is really just meant to be illustrative.
Agreed, though maybe 4 K rather than just a fraction, depending on the contribution from the lower half of the atmosphere. I wasn’t sure how it would turn out in practice, so it’s nice to see these details and their sensitivity to the assumptions. Looks like an interesting source of problems for students in meteorology and related subjects.
However, even in equilibrium one can determine the influences of the different processes to determine what their radiative forcings would be.
Yes, but the concept changes discontinuously at the limit. You have a concept that mathematically has a limiting value of zero and yet that in the limit is far from zero. So in the limit you have one concept with two values, zero and a large number.
VP,
No, I don’t think I do but I’ve been up since very early this morning so may have to leave this till tomorrow to elaborate.
Here are definitions for two concepts of forcing, I’ll call them current forcing and total forcing.
Current forcing: Equilibrium OLR minus current OLR.
Total forcing. Current OLR minus the forcing that would result from adding the current forcing agent to the system when in equilibrium without the current forcing agent.
I associate the former with your value of 3.7 W/m2 and the latter with 150 W/m2 (in the case when current OLR happens to be equilibrium OLR, but I’ve defined “Total forcing” to be more general).
One obvious difference is that equilibrium for the former definition enters with the forcing agent while equilibrium for the latter enters without it. Another is that current OLR is on the right of the minus sign in the former definition and on the left in the latter (or doesn’t exist in the latter definition if you replace it by “equilibrium OLR” for a more specialized notion).
Vaughan, Context/Earth is a project by a name you may recognize from various climate sites – WebHubTelescope. In his own words from a comment at SkepticalScience, “ I have been doing my own time-series “reanalysis” via what I refer to as the CSALT model. This recreates the temperature record via non-temperature measurements such as CO2, SOI, Aerosols, LOD, and TSI (thus the acronym).”
Quite interesting is that WHT has taken his equations and applied them to historical proxy records: “After calibration of recent coral growth to modern equatorial sea-surface temperature (SST) records, the correlation is expected to sustain back through history. This makes it an adequate proxy representation for the Southern Oscillation Index (SOI) that we have been using to understand and potentially predict ENSO dynamics.
The verification experiment is to take several sets of coral measurements and determine if the same general Mathieu-equation fit that was used to model the SOI data could be applied universally. The answer is yes, the SOIM essentially uses similar parameters for the 12th, 14th, and 17th century ENSO proxy data.”
From which he concludes, “What this analysis substantiates is that the underlying dynamics of ENSO maps to the same nonlinear differential equation regardless of the time frame, making it likely a highly stationary process. The ENSO sloshing behavior is thus not a purely chaotic process, but again likely the result of a periodic external force acting on a nonlinear system which destroys the chaos and results in a quasi-periodic regime.”
The sloshing motion of the ocean (the Chandler Wobble), in concert with a few other tidal forces, seems very close to putting a physical explanation on the difference you noted in the Land+Sea, Land-Sea data.
Sorry – forgot to close italics (TWICE!). The last paragraph above is my comment.
Anders:
re surface temperature, I believe Vaughn’s original scenario set the surface of the Earth to have perfect thermal conductivity, which guarantees that there is no diurnal cycle, and that all latitudes have the same temperature.
Further, you say:
The radiative forcing is set at the effective altitude of radiation to space, which is approx 3.3 km in the no foil case, and 10 km for the foil. Taking your formula to apply to skin temperatures rather than surface temperatures, it would be correct.
Kevin,
I’ve closed the italics tags. Can you let me know if I got it wrong?
Thanks, Rachel. You have it correct.
@TC: The radiative forcing is set at the effective altitude of radiation to space, which is approx 3.3 km in the no foil case
That would be for the case when the GHE adds 33K to the effective temperature (no matter what the albedo). It looked to me as though Anders was going with zero GHE as per my problem, for which the effective altitude is zero.
VP,
These are still the same basic concept. If there was no greenhouse effect, the planet would emit to space from its surface and the temperature would be 255 K. The top-of-the-atmosphere would be the surface of the planet. If we then add all the greenhouse gases, this will produce an energy imbalance and the system will return to energy balance when the surface temperature has increased by 33K and when the surface is therefore emitting 150 Wm-2 more than it was in the absence of the greenhouse effect. The radiative forcing of the greenhouse gases is therefore 150 Wm-2 (i.e., prior to the surface starting to warm it would have an energy imbalance of 150 Wm-2).
If we consider the 3.7 Wm-2 case, then that applies to our atmosphere today. Today we emit to space from about 5 km where the temperature will be 255 K (I know it’s not quite this simple, but it’s fine for this). Now add enough greenhouse gases to reduce the outgoing flux at this altitude by 3.7 Wm-2. As we’ve already discussed this can be compensated for by an increase in temperature of 1K (i.e.,
). If the lapse rate is unchanged, then the temperature will increase by 1K at all altitudes (including the surface) and the planet will emit to space from a slightly higher altitude where it is know 255K. So GHGs that produce a radiative forcing of 3.7 Wm-2 (i.e., producing an energy imbalance of 3.7Wm-2) will lead – by itself – an increase in temperature of 1K.
So, I think these two examples are essentially the same basic concept but I may not have done a particularly good job of explaining it.
Tom,
I think Vaughan’s example has no GHGs and so the day-side emits from the surface, not from 3.3km.
@KO’N: Vaughan, Context/Earth is a project by a name you may recognize from various climate sites – WebHubTelescope.
Oh duh, my inference engine must have been down for maintenance: I didn’t recognize WHT’s site. “The Oil Conundrum” should have tipped me off.
CSALT is in a sense complementary to what I’ve been trying to do. Whereas CSALT (as I understand it) aims to develop a comprehensive climate model from as much climate-relevant data as possible, I try to analyze 20-year climate between 1850 and now with as few components as possible and as naively as possible.
My best shot at this can be seen here. 20-year climate CLIM20 is taken to be HadCRUT4 smoothed to a 20-year running mean, hence from 1860 to 2004. AGW is 1.9*log2(co2/280) where co2 is estimated CO2 in ppmv between 1860 and 2004. AMO is CLIM20 − AGW smoothed with a Gaussian filter. Residue = CLIM20 − (AGW + AMO), mainly the leakage resulting from using a running-mean filter (because that’s how 20-year climate is defined) instead of a Gaussian filter.
@ATTP: These are still the same basic concept.
“Same basic” and “same” are different. Dollars and euros are the same basic concept but they’re not the same.
VP,
Okay, I’ll make it stronger. They’re the same concept. They’re both how some effect influences the planetary energy balance prior to any temperature response that will drive us back to energy balance. In a simple sense, that is all that a radiative forcing is. The change in radiative forcing of the GHGs that produce the greenhouse effect is 150 Wm-2. This change in radiative forcing produces an increase in surface temperatures of 33 K. Today, a change in radiative forcing of 3.7 Wm-2 will – by itself – change surface temperatures by 1K.
I think Vaughan’s example has no GHGs and so the day-side emits from the surface, not from 3.3km.
Yes, exactly.
ATTP,
Note that adding all the GHEs (and perhaps also clouds) to the cold atmosphere will lead to a large forcing, but not to the same value that differentiates the present surface temperature from the effective radiative temperature. The values are surely of the same order of magnitude, but not equal. A difference of tens of percent is likely.
Removing all GHEs and all IR influence of clouds from the present atmosphere leads to the negative forcing of -150 W/m^2 assuming that the albedo for SW remains miraculously at the present value. That’s the only strength of forcing directly connected to the value of 150 W/m^2 calculated as you did.
This is the problem I have with quantitative statements about the total forcing.
Pekka,
Sure, I was avoiding differences of 10% or so. I’ll try to add caveats in future, when I remember.
You’re welcome to have a problem (that’s your right), but avoiding this issue would probably mean never quantifying anything. It’s too complex for a blog comment to get it absolutely right. Personally, if I can get it to within about 10%, that’s pretty good given the complexity of the system. The alternative would be to not attempt to quantify anything and that would seem a rather unfortunate way to proceed.
The change in radiative forcing of the GHGs that produce the greenhouse effect is 150 Wm-2.
Yes, but that’s when it’s in disequilibrium. When it’s 99% of the way to equilibrium there’s still 1.5 W/m2 of forcing. When it’s 100% of the way to equilibrium, instead of admittnig that the forcing has finally decreased to zero, suddenly you jump back to a time to when it was first in disequilibrium and declare that there is 150 W/m2 at the time of equilibrium. Your justification of this is to point to when it was first in disequilibrium.
You’re trying to have your cake (150 W/m2 of forcing at initial disequilibrium) and eat it too (0 W/m2 at equilibrium). You’re contradicting the latter and saying, oh no, the forcing at equilibrium is what it was back when it was first in disequilibrium. That’s inconsistent.
VP,
No, that’s not what I’m suggesting, even if it seems that way. The radiative influence of the GHGs, for example, stays the same. The temperature response to this forcing reduces the energy imbalance such that it tends to zero, but that doesn’t change the radiative influence of the GHGs.
I should probably have been more careful in my use of the term forcing. As I tried to explain earlier, “forcing” normally refers to some external driver (GHGs, the Sun, volcanoes,…) and the response to that forcing is a feedback. So, in the case of the greenhouse effect one can regard all the greenhouse gases in the atmosphere as being external drivers that produce a change in radiative forcing of about 150 Wm-2 (give or take 10%). The increase in surface temperature that is a response to that change in radiative forcing is a negative feedback that acts to reduce the energy imbalance back to zero. So, even in equilibrium we can regard the GHGs as producing a radiative forcing of 150 Wm-2 and the increased surface temperature as being a feedback of -150 Wm-2 that balances that radiative forcing.
In the case of anthropogenic global warming, it’s a little more complex. Volcanoes, the Sun, anthropogenic emissions,… are regarded as external drivers that produce radiative forcings. Increases in water vapour and changes in clouds and other responses to these drivers are regarded as feedbacks, as is the increase in temperature (which produces a negative feedback).
If we return to the article that this post was about, the author suggested that a change in surface temperature of 5 degrees would be associated with a change in radiative forcing of 19 Wm-2 (5 x 3.7 Wm-2). Although the number is probably about right, the terminology is wrong as the 19Wm-2 would really be a combination of changes in radiative forcings (from GHGs and albedo changes) and feedback responses (water vapour,…) to those changes in radiative forcing.
VP,
I’ll add that you seem to be suggesting that this is somehow my terminology. I may not be using it is accurately/precisely as I should be, but what I’m trying to do is use standard terminology (as would be used by the IPCC, for example). So, I’m not making up the term “radiative forcing”; it’s been defined by others. I may not be quite expressing myself as clearly as I should be, but that doesn’t mean that the concept of a radiative forcing isn’t clear.
So, even in equilibrium we can regard the GHGs as producing a radiative forcing of 150 Wm-2 and the increased surface temperature as being a feedback of -150 Wm-2 that balances that radiative forcing.
Fine. So what is the radiative forcing just before equilibrium, where there is an imbalance of 1 W/m2 between OLR now and OLR at equilibrium? According to you it’s still 150 W/m2 because the GHGs are producing that much radiative forcing.
Thanks Kevin, I am using the blog http://ContextEarth.com as a kind of research notebook. Many of us are here to put the pieces of the climate jigsaw puzzle together and we all realize that a single blog posting won’t do the trick.
What I did with my previous blog http://mobjectivist.blogspot.com, which was research on oil depletion, was to collect the blog postings into a markup document so I could do the math formatting properly and then released it as an on online PDF document called “The Oil ConunDrum”, which is available via Google Books. After that was finished I closed up the blog and moved on to another one.
My interest is really into trying to capture as large of the picture as is possible and see how all the pieces reinforce each other in a comprehensive document. The problem on submitting this kind of work to a peer-reviewed journal is that no one will consider it because of its size.
Another alternative is to do what John Carlos Baez is doing with his Azimuth Project. Right now, we are pulling together a project to predict El Nino activity, based on people’s talents for doing different kinds of analyses. As the project progresses, the contents are placed in a Wiki, which does a good job of connecting the pieces in a nonlinear fashion. This is arguably better than blog postings, where it is considered bad practice to historically revise too much.
That said I guess my point is that people who read research blogs have to remember that they are a snapshot in time and the trick is to always scan forwards in time.
Let me try a different approach. Here are two definitions of radiative forcing.
1. IPCC (AR5):
Radiative forcing is the change in the net, downward minus upward, radiative flux (expressed in W m–2) at the tropopause or top of atmosphere due to a change in an external driver of climate change, such as, for example, a change in the concentration of carbon dioxide or the output of the Sun. Sometimes internal drivers are still treated as forcings even though they result from the alteration in climate, for example aerosol or greenhouse gas changes in paleoclimates. The traditional radiative forcing is computed with all tropospheric properties held fixed at their unperturbed values, and after allowing for stratospheric temperatures, if perturbed, to readjust to radiative-dynamical equilibrium. Radiative forcing is called instantaneous if no change in stratospheric temperature is accounted for. The radiative forcing once rapid adjustments are accounted for is termed the effective radiative forcing. For the purposes of this report, radiative forcing is further defined as the change relative to the year 1750 and, unless otherwise noted, refers to a global and annual average value. Radiative forcing is not to be confused with cloud radiative forcing, which describes an unrelated measure of the impact of clouds on the radiative flux at the top of the atmosphere.
(Bold mine.)
2. Wikipedia article on radiative forcing:
Radiative forcing or climate forcing, is defined as the difference of radiant energy (sunlight) received by the Earth and energy radiated back to space.
Do you view them as defining the same thing?
WHT: Right now, we are pulling together a project to predict El Nino activity,
This has the big advantage of only having to wait 3-5 years to evaluate any given projection. 20-year climate changes more slowly making short-term predictions vacuous no-brainers, so you have to wait longer to nontrivially test a model’s predictive power.
ATTP,
I have no problems with imprecise numerical values. The only thing I’m hoping for is more precise use of language. In this thread two different values for the forcing that corresponds to 5K temperature change were discussed. Such a discussion is clearly quantitative and the resolution dependent on the precise definition of the concept. Then the discussion was extended to total forcing, but what is total forcing, when it could be defined in many different ways.
As I wrote already, it’s a reality that imprecise use of language, when numerical values are presented, leads to a lot of confusion and unnecessary argumentation in net discussions. A little more care in formulation would often help in keeping the discussion in real issues rather than in figuring out the sources of mutual misunderstanding. Adding words and making text more difficult to read is not the solution, but some extra thought in choosing words that are less likely to mislead part of the readers to an interpretation different from what the writer has in mind.
I understood the main point of the gedankenexperiment of Vaughan to be exactly the point that the original formulation leaves much open for each to fill in a different way. Thus arguing only on the final value would be pointless, but discussing mechanisms that contribute and presenting estimates for them stating the inputs used is more meaningful.
Pekka,
Okay, fair enough.
VP,
Give or take, 10%, yes the radiative forcing of the GHGs is still 150 Wm-2. However, the negative feedback due to the change in temperature is -149 Wm-2 and, therefore, the imbalance is 1 Wm-2.
I think the idea is to think in terms of something that applies a force to the system, which then responds. For example if I had a box on a table with one side attached to a spring that was fixed on the other side, one could apply a force to the other side of the box and it would move and then stop (because the spring would eventually apply an equal and opposite force to the applied force). When stopped, there would be no net force on the box, but one could still measure how compressed the spring is to determine the magnitude of the imposed force.
The importance – for AGW at least – of radiative forcings is that if we can determine how the system responds to a change in radiative forcing, we can estimate how we will warm as we continue to increase our emissions.
VP,
As far as your comparison of the definitions of radiative forcings, then I do see them as the same, although the IPCC makes clear that in their document the change in radiative forcing is measured relative to 1750. That doesn’t really change that the IPCC definition still represents how some change will influence the TOA energy imbalance measured – in their case – relative to 1750. I can see why you might think they’re different, but explained properly I don’t think that they really are.
Anders, the two definitions are quite different. The IPCC definition is the correct definition of radiative forcing as used in climate science. The wikipedia definition amounts to a definition of the top of atmosphere energy imbalance, or the Net Flux. The net TOA flux equals the heat gain in the system, so the two concepts are related by the formula (1) from Gregory et al (2002):
F(t) = Q(t) – λΔT(t)
A certain flexibility in the use of the term “radiative forcing” is OK because what is meant can be understood by context, and scenarios can be set up in which the radiative forcing corresponds to what is examined. However, we do have to keep the basic concepts straight in our heads.
Tom,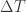
is zero which – I think – would make the two largely the same (i.e., how does some change influence the net TOA flux in the absence of a temperature response).
Yes, okay. I was assuming that in the latter case,
@PP: I understood the main point of the gedankenexperiment of Vaughan to be exactly the point that the original formulation leaves much open for each to fill in a different way.
While the variety of solutions may have created that impression, actually I’d hoped to leave no such wiggle room in my formulation of this (very artificial) problem, whose intended point was rather to exercise concepts relevant to Venus’s clouds when its GHG atmosphere was replaced by an equivalent non-GHE one. I made the foil hemispherical to allow the Sun to heat the Earth because at the time it seemed that a high spherical cloud of completely opaque aerosols that allowed the surface to warm would be hard to specify in enough detail as to admit a unique (non-controversial) solution that could be obtained at least numerically if not analytically. Tom’s “I will leave simplifying it to people with more experience in algebra than my limited exposure.” seemed to assume that the problem needed to be solved analytically, but in this case a numerical solution (with nine iterations of the two formulas) sufficed. (Although quartics–but not quintics—can be solved analytically, doing so would have given the impression that the problem was unreasonably hard.)
As it turned out I’d neglected to include the assumption that the atmosphere had enough heat capacity and fluidity to maintain the foil at 100 degrees below the surface. On the slightly weaker assumption that the cooling foil would cool the nighttime atmosphere uniformly, Anders correctly calculated (other than for using the wrong radiation from the foil) that this would be the case anyway to within a fraction of a degree, which I elaborated on with the point that nonuniform cooling plus the lower heat capacity of the upper atmosphere below the foil might permit the foil to cool by several degrees, or considerably more if the destabilized atmosphere immediately below the foil was sufficiently slow to stabilize. (Though that’s hard to imagine with the foil zipping past at a thousand miles an hour.)
So inadvertently that point was made, albeit not by design, leaving wiggle room to fill in details implying a slightly reduced foil temperature. All other “fill-ins” resulted from either errors or modifications to the assumptions such as GHGs, a nonzero albedo, etc.
@ATTP: However, the negative feedback due to the change in temperature is -149 Wm-2 and, therefore, the imbalance is 1 Wm-2.
If we go with the IPCC definition of radiative forcing then I’m fine with referring to what Wikipedia calls “radiative forcing” as imbalance.
Obviously we’re all in agreement that there is only one mechanism here, just as a motorcycle engine has only one connecting rod. However one cannot then infer that there is only one notion of velocity of the connecting rod. One end oscillates and the other rotates and so to avoid confusion one needs two terms: velocity of the piston end and velocity of the crankshaft end.
In fairness to Wikipedia the body of the article gives the IPCC definition. However that entails an inconsistency with the first sentence of the lead. There’s a lot of discussion on the article’s talk page some of which looks like the result of inconsistent terminology and some the result of disagreement as to what’s actually going on.