I thought I would update my Bayesian climate sensitivity estimate, given the comments I received (peer-review in action). Based on James’s comment, I’ve removed the noise term and am now using the aerosol forcing as the forcing uncertainty. Based on Paul’s comment, I’m using the CMIP5 RCP forcing data, which you can get from here (Specifically, I’ve used the RCP6 forcing data).
I’m still using the Cowtan and Way global surface temperature data, which you can get from here, but I’m using the full HadCRUT4 uncertainties, which you can access here. I’m also still using the 0-2000m Ocean Heat Content (OHC) data from Zanna et al. (2019), which you can get here. I’ve doubled the OHC uncertainties.
Just to remind people, I’m using a simple two-box model:
![C_1 \dfrac{d T}{dt} = F(t) - \beta T(t) - \gamma \left[T(t) - T_o(t) \right],](https://s0.wp.com/latex.php?latex=C_1+%5Cdfrac%7Bd+T%7D%7Bdt%7D+%3D+F%28t%29+-+%5Cbeta+T%28t%29+-+%5Cgamma+%5Cleft%5BT%28t%29+-+T_o%28t%29+%5Cright%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002)
![C_2 \dfrac{d T_o}{dt} = \gamma \left[ T(t) - T_o(t) \right],](https://s0.wp.com/latex.php?latex=C_2+%5Cdfrac%7Bd+T_o%7D%7Bdt%7D+%3D+%5Cgamma+%5Cleft%5B+T%28t%29+-+T_o%28t%29+%5Cright%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002)
where the upper box is the ocean’s mixed layer and atmosphere, and the lower box is the ocean down to 2000m. I’m going to be lazy and not describe all the parameters and variables, which are described in my previous post. I’m fitting my model using Markov Chain Monte Carlo, which I’m doing using a python package called emcee.
The figure on the top right shows the fit to the surface temperature data, while the figure on the bottom right shows the fit to the 0-2000m OHC data. In both cases, the orange curve is the median result, while the grey lines sample the range.
Below is a corner plot showing the resulting distribution for the parameters. The parameter 
The table below shows the results for the Equilibrium Climate Sensitivity (ECS), Transient Climate Response (TCR), ECS-to-TCR ratio, and the heat capacity of the upper box. Since the 
| Parameter | 15th percentile | median | 84th percential |
|---|---|---|---|
| ECS (K) | 1.92 | 2.18 | 2.47 |
| ECS (K) – |
2.06 | 2.25 | 2.47 |
| TCR (K) | 1.55 | 1.74 | 1.94 |
| TCR (K) – |
1.48 | 1.59 | 1.73 |
| TCR-to-ECS ratio | 0.75 | 0.80 | 0.85 |
| TCR-to-ECS ratio – |
0.68 | 0.71 | 0.75 |
|
3.85 | 4.73 | 5.70 |
This updated analysis has narrowed the range for both the ECS and TCR, and brought the upper end down somewhat. However, the median estimate for the ECS is still above 2K, and the lower limit (15th percentile) is still close to 2K. The figures on the right show the resulting ECS and TCR distributions.
Having now updated my analysis, I will probably stop here. I do have some other work I need to focus on. James has suggested that he is working on a similar analysis, so it will be interesting to see the results from this work and how it compares to what I’ve presented here.
Update:
As per Peter’s comment, I’ve redone the analysis using Lijing Cheng’s OHC data, which starts in 1940. I’ve also assumed a constant heat capacity for the upper box of
| Parameter | 15th percentile | median | 84th percential |
|---|---|---|---|
| ECS (K) | 2.08 | 2.36 | 2.64 |
| TCR (K) | 1.44 | 1.58 | 1.72 |
| TCR-to-ECS ratio | 0.63 | 0.67 | 0.71 |
Update number 2:
I had forgotten that I meant to mention that I’d had an email from Philip Goodwin who has also done similar analyses. For example, in this paper that I actually discussed in this post. There is also a recent paper by Skeie et al. (2018) that also uses MCMC, as does this paper by Bodman and Jones.
...and Then There's Physics 
Below is a comparison of the 0-2000m OHC increase for 2005–>2018; Zanna et. al and NODC (zetajoules):
Zanna et. al. — 71
NODC — 139
Worth checking, since that is a bigger difference than I was expecting.
https://www.nodc.noaa.gov/OC5/3M_HEAT_CONTENT/basin_data.html
Chubbs,
Yes, that is a bigger difference that I would have expected.
yes, the provenance of and sensitivity to the OHC data were going to be my first question. Lijing Cheng has an OHC data product increasingly used in climate studies: http://159.226.119.60/cheng/
Peter,
I have done some analyses with Lijing Cheng’s data. I will post that in a later comment.
If one could see inside the blue and red lines, the one we are on, I suspect one would see a series of this S diagram in miniature. We spent the first 15 years of the 21st century on the blue branch; now we’re on the red.
My only real criticism of your work is this figure circa (1992-2018) …
The slope (or rate of OHC) appears to be quite high with respect to the observations. IMHO this is dangerous if one uses the OHC model results as a starting point for extrapolation (using assumed future forcing time series) beyond 2018 (IMHO the semi-empirical SLR models suffered from somewhat similar high starting off point and slopes (relative to observations)).
Otherwise, way above my pay grade, but AFAIK, a very nice effort. 🙂
Peter,
I’ve updated the end of the post with an analysis that uses Lijing Cheng’s 0-2000m OHC data, rather than the data from Zanna et al. (2019). It pushes the ECS results up a little, but doesn’t change the TCR results much (because the ECS-to-TCR ratio goes down).
EFS,
I’m not quite sure what you mean by “beyond 2018”. In principle this analysis is fitting the temperature and OHC data at the same time. However, I have doubled the OHC uncertainties, so that probably means that the fit to the temperature data is dominating a little. However, if you check the update to the post, I have redone the analysis with Lijing Cheng’s data, which now shows a better median fit to the OHC data, but the range is quite broad.
ATTP,
The new analysis with Cheng data isn’t that far from a climate model considering effective climate sensitivity is less than equilibrium and aerosols probably introduce a low bias. Note that the model fit appears to be falling behind the recent rise in temperature and OHC.
Thanks for the link to Isaac Held’s blog on 2-box model in the previous post. After reading his blog, not surprising that the box sizes don’t necessarily match the real world. Per Held, deep ocean mixing is not linear and is not closely tied to the global average temperature. Below is one of his quotes:
“….the coupling to the deep oceans is strongest in the North Atlantic and the Southern Oceans, so the temperature anomalies in those regions presumably have more to do with the uptake than the global mean. Only if the forced warming is separable in space and time — T(x,t) \approx\ A(x)B(t) do we have any reason to expect the uptake to scale with the global mean temperature. A changing mix of greenhouse gas and aerosol forcing is the easiest way to break this separability.”
Per Held’s early series of blogs, makes much more sense to estimate TCR from observations than ECS. The top ocean box has roughly linear mixing, i.e. Delta T/Delta F is a constant. Observations from the recent forcing ramp indicate TCR is around 1.8, close to the climate model estimate. Going back further in time lowers the TCR# somewhat, but why bother, since aerosol uncertainty increases rapidly before 1970.
Diffusion is physically an infinite-box model, i.e. realistically described as an infinite set of slabs stacked on top of each other. A 2-box model leads to a damped exponential in time, which is a far cry from the Fickian fat-tail of realistic diffusion as the heat diffuses to the depths of the ocean.
What Hansen estimated in 1980, a vertical diffusivity of ~1 cm^2/s, still holds true:
Chubbs,
Yes, it’s not really a surprise that the results from this simple model don’t quite match the real world.
If you are using the full HadCRUT4 uncertainty and aren’t taking into account the coverage uncertainty of Cowtan and Way, then you aren’t taking into account the full uncertainty.
In this post, you have lower climate sensitivity estimates than before. Is the difference primarily due to treatment of aerosols?
“The results from this simple model don’t quite match the real world.”
Sounds familiar even after decades of Moore’s Law at work–
Click to access co2.pdf
-1,
Yes, I realise that I may not be taking all the uncertainty into account, but I wasn’t sure how to include the additional uncertainty. However, I’ve just noticed that the Cowtan and Way data does include coverage uncertainty, so maybe I’ll add that. I don’t think the different is due to aerosols (I was already including that in the previous analysis). It might be the change in forcing dataset. I started this quite a few months ago and when I wrote up the last one I couldn’t work out where I’d got the forcings from. I’m now using the RCP forcings.
-1,
If I include the coverage uncertainty, then it reduces the ECS a little, but not much.
Pingback: An attempt to do a Bayesian estimate of climate sensitivity | …and Then There's Physics
Are the observational uncertainties treated as if the associated errors (measurement, bias, coverage etc.) were correlated or uncorrelated?
John,
In this analysis, the uncertainties are uncorrelated. I presume, though, that the HadCRUT4 total uncertainty is determined based on the associated errors being correlated.
I have to say, this is all so typical of discussions on “warmist” eco-mentalist blogs. Whenever anyone presents some “science”, the denizens swallow it hook-line-and-sinker, without any sort of self-scepticism or attempt at critical review. [something about bubbles and echo chambers… blah blah blah]
… oh, sorry, that was yesterday, wasn’t it? ;o)
Another excellent blog post and comments thread. I have a project that would be good for emcee, but I need to evolve out of my dinosaur MATLAB habitat! ;o)
Again, I think that the key test would be to apply this to a climate model. It would take some work to figure out how to develop an “observed” ocean heat content, surface temperature dataset, and forcing time series in model world of comparable quality to our own observed data, but once you did that, you could see how often your model could correctly diagnose the climate sensitivity of the model. (I’m not sure you were on my wavelength with my previous comment: I wasn’t suggesting comparing the pdf of CS from your analysis to the pdf of CS from CMIP5 or CMIP6… I was suggesting running the full Bayesian analysis on each CMIP5 model, and seeing where in each generated pdf the actual model sensitivity fell. If your approach was perfect, you’d expect that your approach would lead to a median that was higher than the real CS half the time, and lower half the time, and that the real CS would fall outside your 15-84 percent bounds about 30% of the time, etc. I’m not suggesting you actually do this: it would be a tremendous amount of work.
Having said that, my guess is that it would turn out that your model is overconfident: I don’t think that the last 120 years of surface & ocean data alone should be enough to constrain equilibrium climate sensitivity to be less than 3 degree with 95% probability… as evidence, I point to a similar-ish approach, using a more complex model in place of an energy-balance model (https://www.adv-stat-clim-meteorol-oceanogr.net/4/19/2018/), that finds a median ECS of 3.7 degrees: the two approaches use similar underlying data, but get very different estimates, which implies not only that at least one of the approaches is off in terms of central estimate, but also in terms of uncertainty bounds.
Some thoughts:
1) your ocean is obviously very simplified… an interesting question is how complex a model needs to be to capture the most important interactions. For example, for fitting historical data, there is some indication that land/ocean temperature patterns could be important, especially in terms of the response to aerosol forcing… so would a 4 box model (deep ocean, upper ocean, atmosphere-over-ocean, atmosphere-over-land) yield substantial differences or not? What about two hemispheres? (also not suggesting you do this: it would be a lot of work, and I presume at some point would become computationally intractable).
2) how are you representing forcing uncertainty? In your previous post, it seemed like it was just a scalar of total forcing… I’d think that at a minimum, it would be a good idea to separate the GHG forcings from the aerosol forcings, and have the latter be more uncertain than the former.
Anyway, I still think this approach is very neat and interesting, just that there are some key caveats, I’d be interested in understanding what would happen with incremental additions of complexity, and in seeing how well this approach performs in a system with a known answer (like a CMIP5 model).
climatemusing,
I’m still not quite sure that I’m following what you’re suggesting here. In a GCM the climate sensitivity is emergent. It’s already well known that if you were to infer climate sensitivity from a climate model using an approach similar to what I’ve done here, there’s a tendency to recover a value that’s lower than the actual model sensitivity.
Agreed. Again, this is mostly due to the assumption that the feedback response (or, in my model,
) is linear. This assumptions does appear to return climate sensitivities that are probably lower than they are in reality.
Your observations about the model are certainly correct. Would be interesting to try a sightly more complex model, but I don’t really have the time to go that far (at the moment, at least).
In this model, I’m simply using the aerosol forcing as the forcing uncertainty. I haven’t, however, separated the actual forcing into the different components, although that would be interesting to try.
The HadCRUT4 bias uncertainties, contain temporal correlations. If you are treating the temporal correlations as uncorrelated then this will result in an underestimate of uncertainty. You could use the temporal correlations between the 100 ensemble members of HadCRUT4, or alternatively between the 100 ensemble members of Cowtan and Way, to take this into account.
Another serious posting gone.
The comments from the Zanna paper are interesting and pertinent to OHC discussions here, you could restore them. My views on OHC being terribly difficult to assess are backed up by your admission of ” I realise that I may not be taking all the uncertainty into account”.
This was the problem with a recent paper elsewhere as we all recall.
It in no way stops you doing an ECS assessment, that’s great, just emphasises the grey area we currently have.
-1,
Yes, I could probably try and take that into account. I wouldn’t be surprised, though, that this analysis under-estimates both the uncertainty and the best estimate.
Dikran,
Feel free to get in touch if you want a hand with this. I’m pretty new to this myself, but it’s actually pretty straightforward to get it started.
Cheers ATTP, may well do that! I had been meaning to investigate STAN (https://mc-stan.org/), but I think that may me rather more than is needed for this particular task.
Nice, looks like the theta 1 parameter is a bit smaller too.
I think these types of estimates will trend upwards quite quickly over the next several years as the statistical influence of “the hiatus” on the end of the record wanes.
Paul,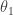
is now about -0.15, which is smaller than the 
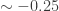that I got with the previous analysis.
Yes, the median value for
I think these types of estimates will trend upwards quite quickly over the next several years as the statistical influence of “the hiatus” on the end of the record wanes. …
If you look at Ghil’s diagram, we are supposedly in the steep part of warmer red phase.
@aTTP:
I have some questions and comments to your Bayesian climate sensitivity estimate.
1) You get an parameter theta_1 for an initial temperature difference between the two boxes.
Is this consistent with the historic temperature development?
That means, if you would run the model with reconstructed temperature data from the last millennia or centuries, would this give a similar value for the temperature response?
Have it at least the right sign or magnitude?
Or does it try with this parameter to compensate some misfit between model and data?
2) What units you use for the heat capacity?
I can not reproduce the value of C_1 = 2 for a 67 m deep ocean.
If I assume a global layer of 67 m water I get C_1= 4.1e6 * 67 / seconds_per_year = 8.7, assuming forcing is in W/m² and temperature is in K and the time is in years. Restricting the ocean layer to 70.7% of the globe does not help.
3) More on heat capacity.
You have written that the first layer represents the upper layer of the ocean plus the atmosphere.
But in the first post, you say using C_1 + C_2 for the heat content of the ocean. This sets the heat capacity of the atmosphere and other components to zero.
Could this be a reason for the high value of C_1?
Compared to the upper ocean layer, the heat capacity other than ocean water is not negligible. If you include not only air but also water vapor, sea ice, and the upper ground layer, and the slower components as glaciers and ice sheets and deeper ground layers, the total heat capacity is similar to several tens of meters of water.
4) You assume an uniform temperature of the first layer T. For the purpose of the ocean heat capacity and the exchange of heat with the lower ocean layer it should be the SST.
But you use the temperature data from Cowtan and Way. This consists of SST only for open sea but SAT for land and sea ice.
The may be a large difference in this data. For example I got for the BEST data a warming of the global SAT by 2018 of 1.2 K compared to the second half of the 19th century but only a warming of 0.75 K for the SST in the same time.
This difference of warming between SST and global SAT may affect the climate sensitivity estimates.
5) There are water below 2000 m which should also uptake some heat from the layer above.
Uli,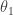
term does seem reasonable. If you multiply it with 
you get about -0.1 W/m^2, which suggests that system is out of balance by about this in the mid-1800s.
1) I have considered running the model from earlier, but haven’t had a chance. The
2) The units should be J/m^2/K. However, you’re correct that I have forgotten to mention that it’s actually in units of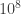
. So you can get it from
where the 1000 is the mass of 1m^3 of water, and the 4000 is the specific heat capacity in J/kg/K.
So,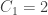
is actually close to 70m, than to 67m.
3) I did try including the mass of the atmosphere (
kg) but it doesn’t make much difference and I don’t think it explains the high 
value. I think this is mainly because I’m assuming it exchanges with quite a massive lower box.
4) Fair point. I hadn’t thought of that.
5) You can include this, but it seems to mostly affect the TCR-to-ECS ratio. I suspect assuming that the entire ocean is one box starts to ge a bit unrealistic.
@aTTP:
1) Why you haven’t had a chance?
2) OK.
3) It’s not only the atmosphere. Sea ice for example.
5) Yes, the TCR-to-ECS ratio may not be very realistic. Also due to not equal distributed forcings.
Uli,
1) Just because I haven’t had a chance to update the code. I’ve been running all of this on my laptop, but there’s another paper I need to finish, so I’ve stopped for the moment.
3) I was thinking a bit more about this, and the upper box is really meant to represent a system that has a total heat capacity of
and a temperature of 
. For a simple model like this, what I’m doing is probably fine. You could get more complex and do something like this model that has multiple boxes and multiple timescales (it actually produces a best estimates ECS of 2.4K and a 2 
range of 1.4K – 4.4K). I just don’t really have the time to code up a more complex model.
ATTP,
Not a bad effort for insight. However, you may want to note the following issues for any future work.
1) The RCP forcing dataset which you are using is ERF and NOT Fa. You can’t use ERF values for temperature prediction, but then use an Fa forcing value of 3.7 for a doubling of CO2 in order to scale the fitted feedback value to an effective ECS. The appropriate value to use should be the ERF value, which is 3.4. This will scale your CS estimates down by 3.4/3.7.
2) The fully explicit numerical scheme you are using produces serious time truncation errors, which affect the reliability of your fitted parameters. The fitting error arises from (a) the sharp volcanic excursions where your scheme introduces a one-way bias relative to the secular variation and (b) the curvature in the secular variation, which is underestimated by the explicit scheme, and which therefore requires a compensatory error in the estimated parameter values. A quick fix for this is to replace your scheme with a RK4 scheme AND to interpolate your input series to use quarter-year timesteps. This reduces the cumulative numerical error to negligible values and greatly reduces the smearing and time-displacement evident in your solutions. You can then re-average the results back to annual values for error calculation and fitting if you wish. It can all be programmed in less than an hour.
A better, but more time-consuming solution is to note that you can substitute out your T0 value to reduce your two simultaneous equations to a second-order linear differential equation in T alone. This then provides an analytic solution for T(t) and for N(t) (total net flux into the ocean) for a constant unit step-forcing. From this, you can use superposition to forward model. The main advantage of this is that, unlike your Euler scheme and RK4, both of which assume continuous and differentiable series, this approach accommodates volcanic forcings and sudden changes in forcing without any “time-smearing”.
(3) Your use of θ1 is not to be recommended in this mathematical model. It has perverse consequences. To understand why, try running your model with all radiative forcings set to zero, but with your deep ocean temperature set one degree cooler (say) than steady state, and have a look at the net flux curve (into the ocean) and the surface temperature curve against time. You will find that initially you will induce a heat flux from the mixed layer into the deep which will cool the mixed layer and start warming the deep, as expected. The reduction in temperature of the mixed layer will induce an increase in net downward radiation via your feedback term. Eventually, the mixed layer temperature falls sufficiently for the increase in net downward radiation to exactly balance the decreasing heat flux from the mixed layer into the deep. At that point the mixed layer achieves its minimum temperature and the net flux into the (total) ocean achieves its maximum value. Thereafter, the flux from the mixed layer into the deep continues to decline because of the reduction in temperature differential, and so the temperature in the mixed layer starts to increase from its minimum value and the net flux into the ocean starts to decrease. Eventually, the temperature in the mixed layer regains its initial value (which balances the radiative flux), the deep ocean has gained one degree of temperature and the net flux into the ocean returns to zero.
The problem which arises is that, while all of the above is completely compatible with he mathematical model, the timings are not compatible with reality and highlight the inadequacy of the simple characterisation of the transfer of heat to the deep in this two-body model. Specifically, with the sort of parameters you are using, it takes only 2 to 3 decades to achieve the minimum mixed-layer temperature and then takes hundreds of years thereafter for the system to restabilise. Consequently, if you initiate your simulation using forcings from 1765 with this starting situation (of the deep being one degree cooler), then a hundred years later, at the start of your matching period, you have imposed a WARMING trend on the surface temperature anomaly data over the matching period, so cold ocean causes warming (!) – highly counterintuitive. The converse is also true. Alternatively, if you impose a temperature difference at the start of your matching period, then you introduce a positive or negative bump over the following decades in both the temperature plot and the net flux plot. This is an artifact of the inadequacy of the description of heat tranfer.
kribaez,
1. Okay, that’s a fair point.
2. I did consider something like this (I use RK4 quite a lot). However, since all my timeseries are annual, I didn’t expect this to make much difference. You may be right that the volcanic excursions could influence the fit.
3. I’ll have to think a bit about this. I did wonder if this parameter could cause some problems, but I don’t entirely follow your thought experiment.
L&C (2014) used 3.71 for 2X CO2 (paper section 5.5), that is the value that matches the CMIP5 forcing values, so disagree with Kribaez.
Chubbs,
You are correct. Moreover L&C (2018) retained this value as a median estimate. It is founded on the median estimate of 1 to 20 year extrapolation of the Net Flux vs Temp plots of the CO2 quadrupling experiments, together with the assertion in AR5 that the ERF value for a doubling of CO2 should be very similar to the Fa value. I honestly thought that this had been challenged and amended as a benchmark, but on checking various sources, the consensus view remains unchanged. ATTP is justified in using his 3.7 value. Thank you for the comment.
kribaez, ATTP: In L/C 18 was used the factor 3.8 W/m² for a doubling of CO2, not 3.7. See section 3a, there is also mentioned the reason for it ( latest forcing data for CH4).
frankclimate,
From S4 of L&C 2018:
“The ensemble-mean 2x CO2 F value from regressing over years 2–10 of the abrupt 4xCO2 simulations is 3.80 Wm−2 before dividing by 1.046 to adjust for the non-logarithmic aspect of CO2 forcing, and 3.63 Wm−2 after doing so.”
The 3.71 value comes from the median of year 1-20 regressions. The 3.8 value comes from the median of year 2 – 10 regressions using the same data and basis. In both instances, they are uncorrected for the non-logarithmic variation of CO2 forcing against concentration.
“As methods of estimating ECShist and ECS do not all involve the same CO2 concentrations,
we allow for the non-logarithmic aspect of CO2 forcing (Etminan et al.2016) when carrying out all
calculations, so that all the ECShist and ECS estimates reflect a doubling of CO2 concentration.”
The change in view of methane forcing, which you mention, affected the historic (and projected) ERF forcing series rather than the estimate of 2xCO2 F, as I understand it This shift of estimated median comes solely from the choice of regression period.
Given some of the other uncertainties, I think ATTP is justified in using 3.7 as a benchmark for the present at least.
kribaez: The forcing due to 2*CO2 depends on the used data set for the antr. forcing. If it’s the revised (CH4 data from Etminan et al 2016) one has tu use the value 3.8 W/m², as it’s mentioned in L/C18, section 3a: “The revised total 1750−2011 anthropogenic forcing estimate has increased by 9% from the AR5 value; the largest contribution comes from the revision in CH4 forcing F2 CO2 has also been revised up by 2.5%, to 3.80 Wm−2, which has an opposing effect on sensitivity estimation to the upward revision in total forcing.”.
If it’s the original dataset from AR5 the value of 3.7 W/m² is justified.
Pingback: 2019: A year in review | …and Then There's Physics
So, after all of that,
It appear that we can reasonably say that as the concentration of atmospheric CO2 increases, atmospheric temp also increases.
NASA estimates that from 1975 to 2018
atmospheric CO2 increases from 280 ppm
To 400 ppm and atmospheric temp increases 1°F.
Is this enough data to model increase
In CO2 = x heat?
Roseland,
The increase from 280ppm started in the 1800s. I’m not quite sure what you’re asking though. There is certainly enough evidence to be confident that adding CO2 will lead to warming. Precisely how much is hard to say, but the tables in the post are estimates of that.